《Streaming Systems》第二章 数据处理的 What，Where，When 和 How

第二章中通过一些具体的例子更详细地介绍了第一章中提到的数据处理模式。这一章涉及了提供可靠的乱序数据处理所需要的核心原则和概念，也就是能够推断时间的一系列工具。

学习路线

本书第一部分（The Beam Model）的大部分以及本章全部内容的讨论会涉及到五个核心概念，其中前两个概念在第一章中已经有所涉及：

1. 事件时间和处理时间 的区别
2. 窗口（windowing）
   窗口是用于处理无界数据源的常用方法。
3. 触发器（Triggers）
   触发器是用于声明何时发出窗口结果的机制。触发器也使得在不同时间多次产生窗口的输出结果成为可能，这可以让我们进一步调整之前的输出结果。
4. 水位线（Watermark）
   水位线是有关事件时间中输入完整性的概念，一个时间值为 X 的水位线意味着：所有事件时间在 X 之前的输入数据都已经被观察到了。水位线是用于跟踪无界数据源处理过程的一个度量值。
5. 聚合（Accumulation）
   聚合模式指定了同一窗口的多个输出结果之间的关系。这些结果可能是完全无关的，也可能是相互重叠的。不同的聚合模式有着不同的语义和开销。

为了更好地理解这些概念之间的关系，可以从回答以下四个问题的角度来加深对这些概念的理解：

• What：需要计算出什么样的结果？答案是通过 pipeline 中不同类型的数据转换。
• Where：结果计算发生在事件时间中的何处？答案是在 pipeline 中所使用的事件时间窗口。
• When：结果在处理时间的何时被发出？答案是所使用的触发器和水位线（可选）。
• How：用于改进最终结果的不同结果之间是怎样关联的？答案是使用的不同的聚合类型：忽略（disgarding）、累积（accumulating）、累积并撤销（accumulating and retracting）

批处理基础：What 和 Where

What：数据转换（Transformations）

本章节以及书中大部分地方都会用到一个简单的例子：在一个有9条数据的数据集上根据键值计算整数和。假设现在有一个基于团队的手机游戏，我们希望构造一个 pipeline 来计算每个团队的分数，团队分数即为团队中每个用户的手机上传的单个分数的总和。

这里假设这9条数据都来自同一个团队，需要关注的属性只有三个：

• 分数：单个事件中的用户得分
• 事件时间：该得分事件发生的时间
• 处理时间：pipeline 观察到该得分的时间

将这9条数据用一个x轴表示事件时间，y轴表示处理时间的静态图表示出来，如下图所示：

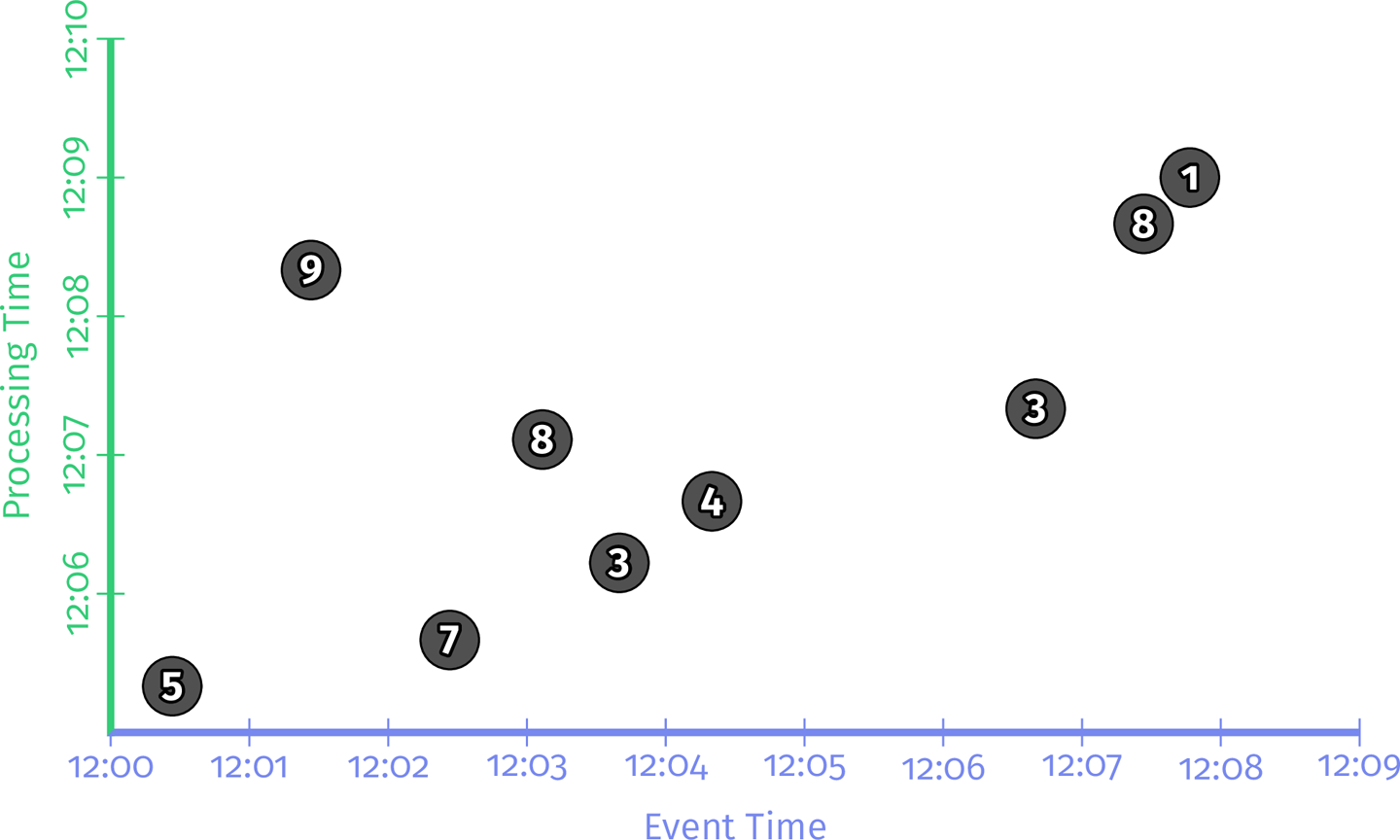
在之后的每个例子中，都会有一小段 Apache Beam Java SDK 的伪代码，用于定义具体的 pipeline。对于一个从 I/O 源读取数据，解析（团队，分数）对，并且计算每个团队总分数的简单 pipeline，样例如下：

PCollection<String> raw = IO.read(...);
PCollection<KV<Team, Integer>> input = raw.apply(new ParseFn());
PCollection<KV<Team, Integer>> totals = 
	input.apply(Sum.integersPerKey());

在描述 pipeline 的代码段之后，会有一张图来展示对于单个键值，pipeline 在指定简单数据集上的处理过程。

图中的x轴表示事件时间，y轴表示处理时间，因此，真实时间是沿y轴从下往上的，这里用一根黑色的水平粗线表示处理时间的递增过程。每个输入是一个圆圈，其中的数字表示得分。这些圆圈在一开始是亮灰色的，进入 pipeline 后颜色会变深。

当 pipeline 发现数据后，它会将这些值累加到中间状态中，最终的聚合状态会作为输出发送出去。状态和输出是用矩形表示的，灰色表示状态，蓝色表示输出。状态聚合结果会显示在矩形上方。

对于上述例子中的 pipeline，在一个经典的批处理引擎上的处理过程如下所图示：

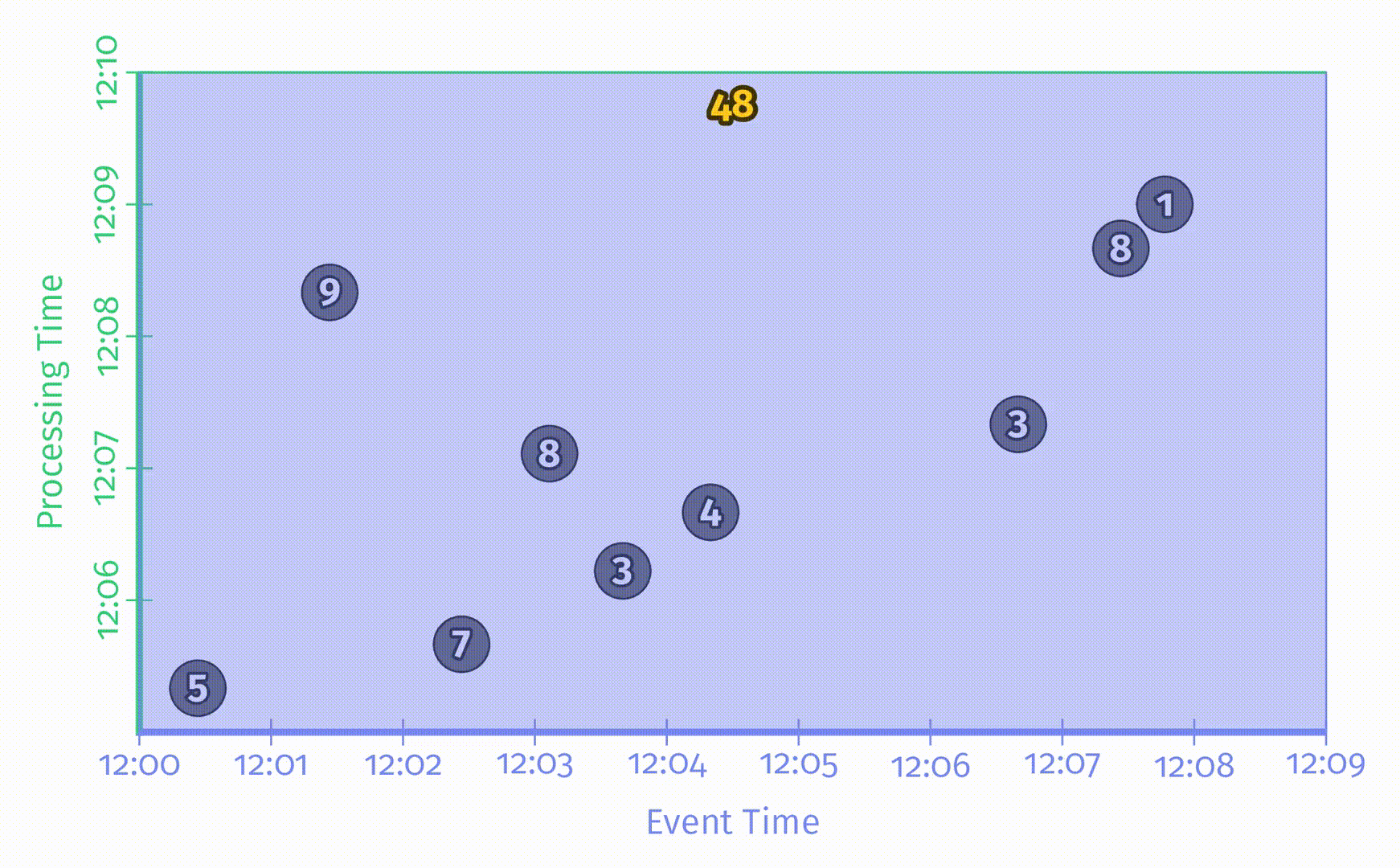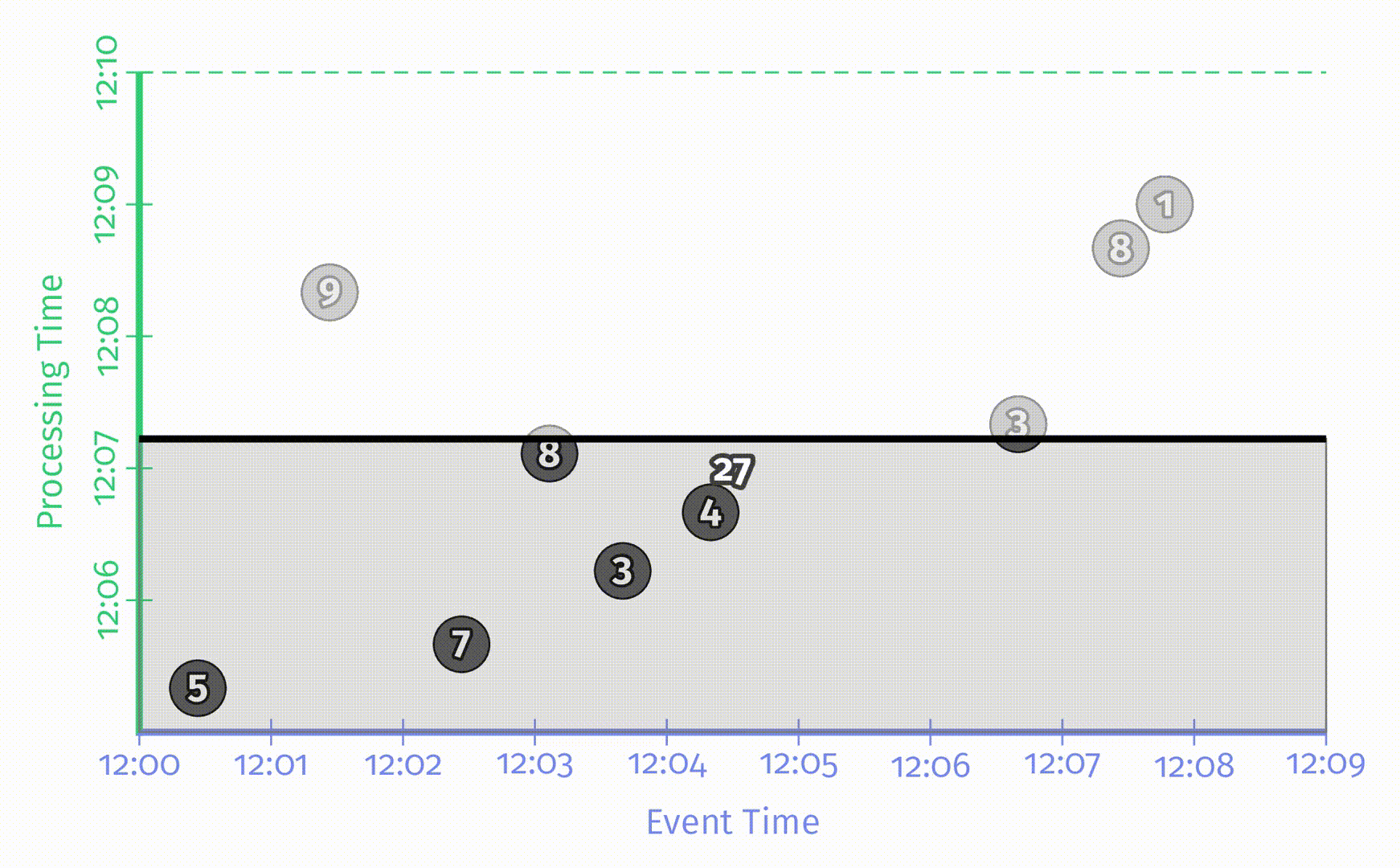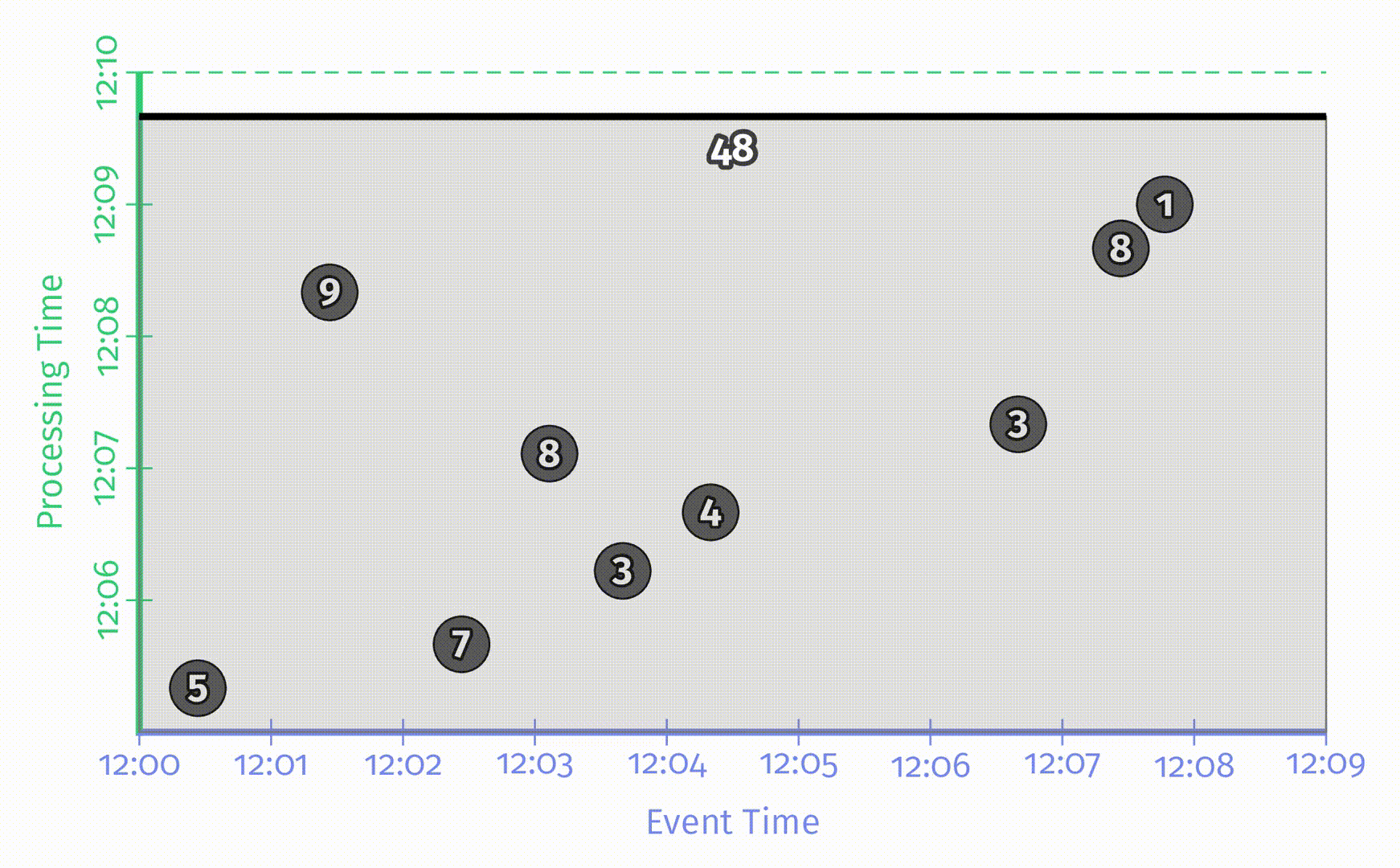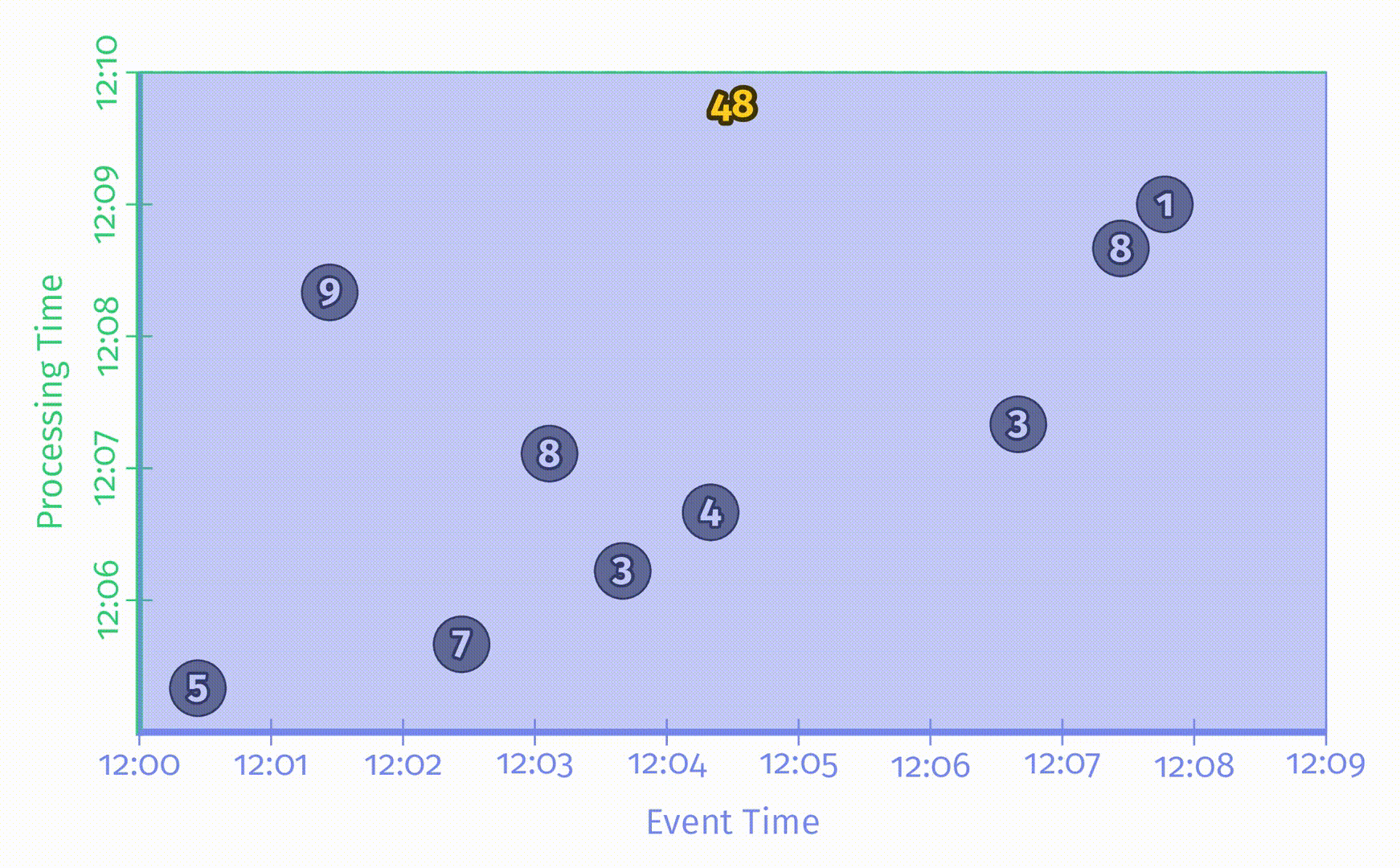
由于这是一个批处理 pipeline，它会不断累加状态直到处理过所有数据（用最上方的绿色虚线表示），最后会输出唯一的结果 48。

Where：窗口

以两分钟的滚动窗口为例，在 Beam 中，只需要简单增加 Window.into 的操作：

PCollections<KV<Team, Integer>> totals = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES)))
	.apply(Sum.integersPerKey());

Beam 提供了可以同时在批处理和流处理中工作的统一模型。在批处理引擎中运行该 pipeline，对应的结果如下：

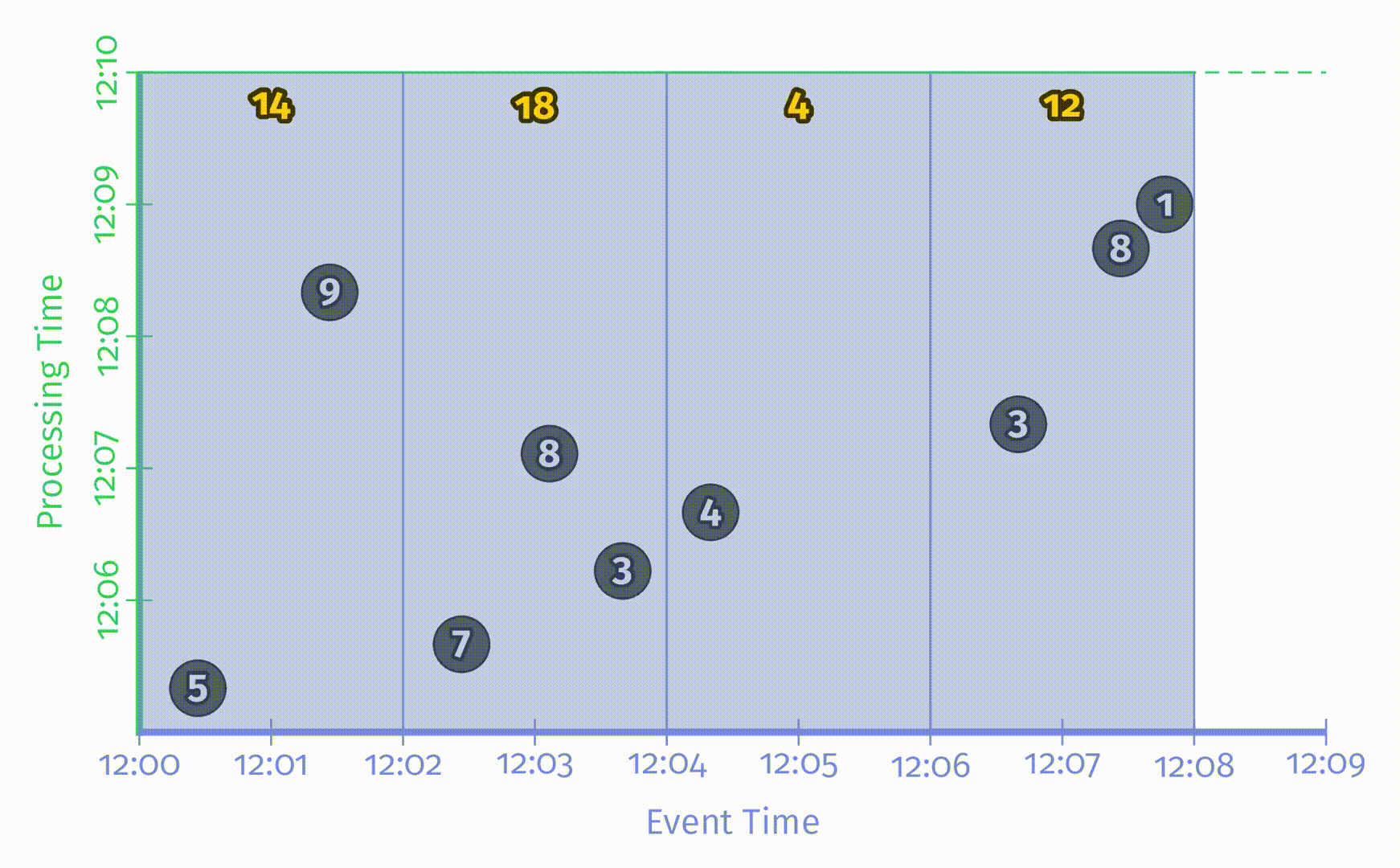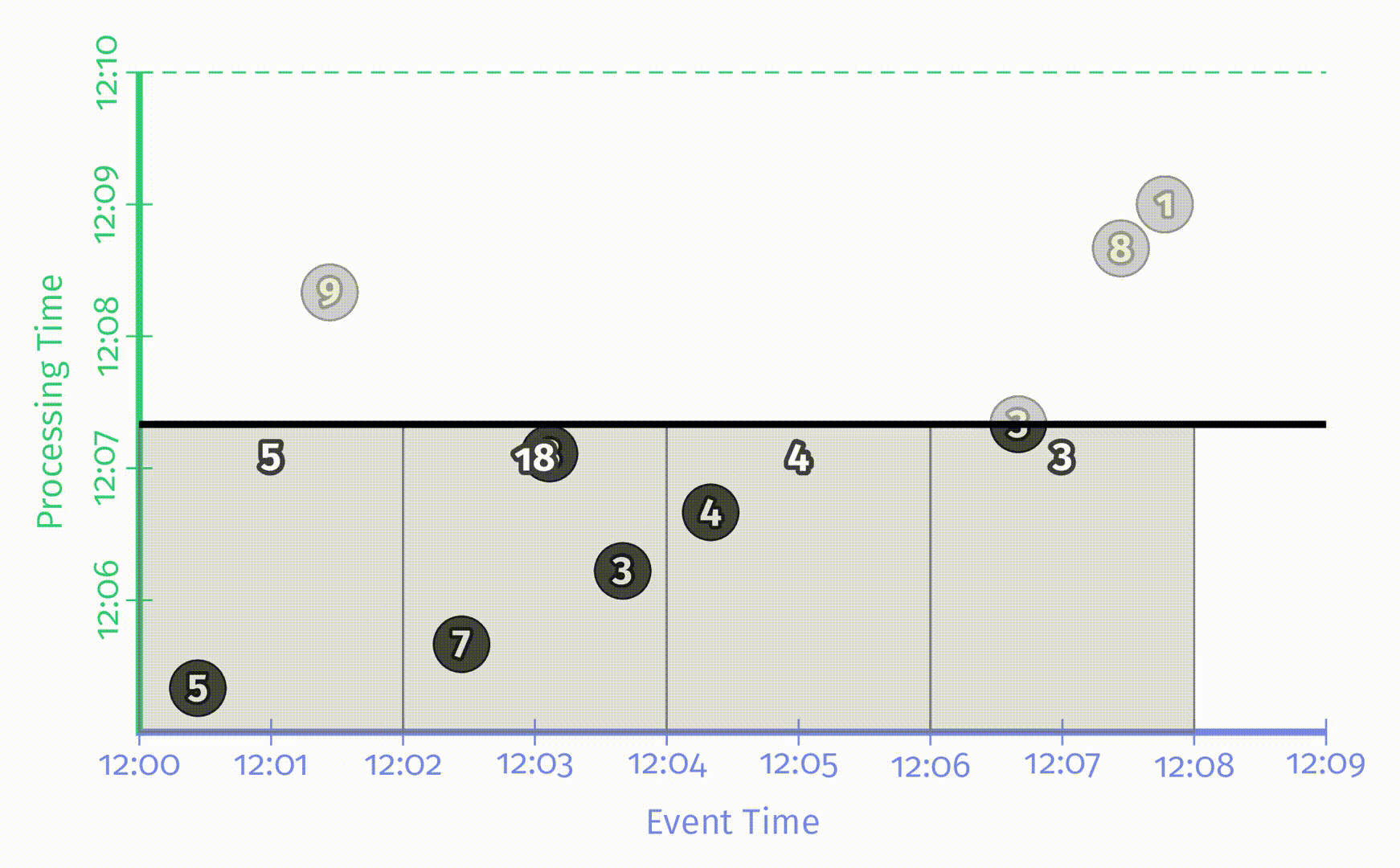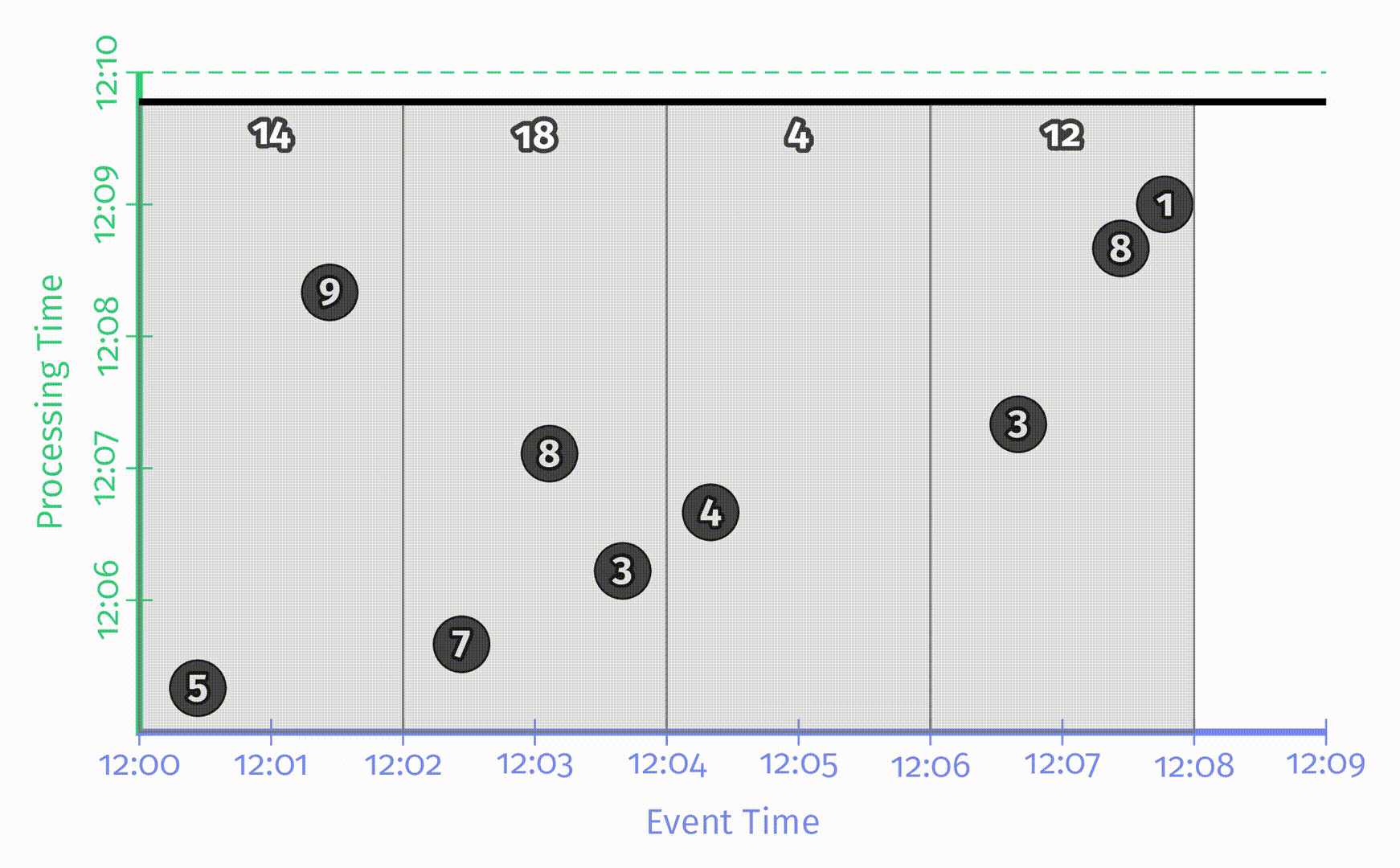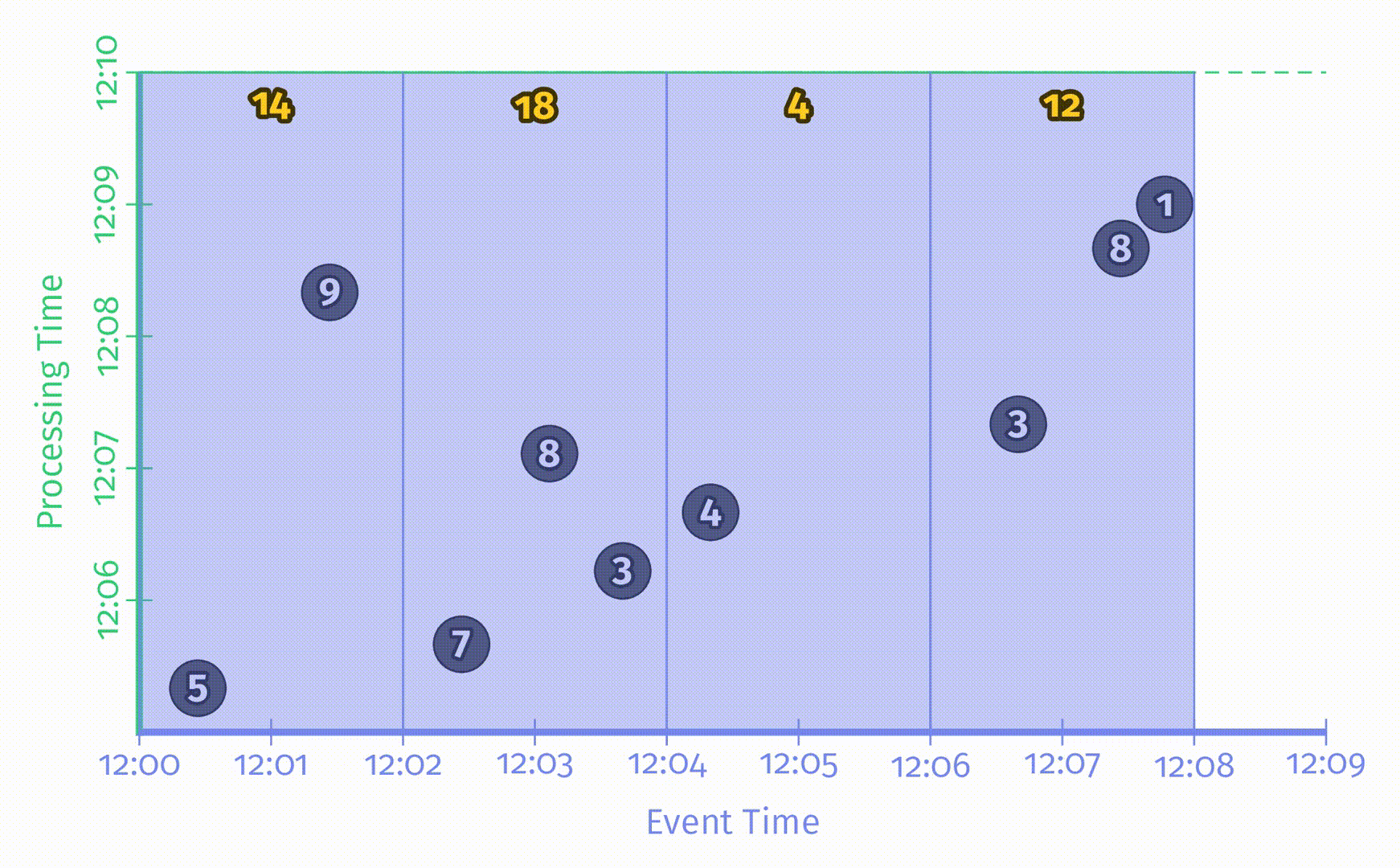
与之前一样，输入被累加到状态中，直到所有输入都被处理完成后才会产生最终输出。有了窗口之后这里会得到4个结果，分别对应着4个两分钟的事件时间窗口。

流处理：When 和 How

When：触发器

触发器声明了在处理时间中窗口的输出应该在何时触发（触发器可能根据其他基于不同类型时间域中的工具来做出该决策，比如基于事件时间的水位线）。

尽管存在着众多可能的触发器语义，但在概念上只有两种通用类型的触发器，实际应用几乎总能归结为使用了其中的一种或两种的组合：

• 重复更新式触发器
  随着窗口中内容的变化，周期性地生成更新后的窗口输出结果。更新可能发生在每个新数据到达后，或者在一定处理时间延迟后；更新周期的选择需要在延迟和处理开销之间做出权衡。
• 完整性触发器
  在一定程度上确认窗口已经包含完整输入后输出窗口计算结果。这与批处理情况很类似：只在输入完整后才输出结果，区别在于这里的完整性范围只是针对单个窗口而非整个数据集。

重复更新式的触发器在流式系统中更为常用，它实现起来更为简单，也更容易理解。

完整性触发器相对来说没有那么常见，但它为流式系统提供了非常接近于批处理系统的语义，并且也提供了处理丢失和迟到数据的工具。

简单起见，首先考察针对每个数据都进行更新的重复更新式触发器：

PCollection<KV<Team, Integer>> total = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES))
		.triggering(Repeatedly(AfterCount(1))))
	.apply(Sum.integersPerKey());

在流处理引擎中运行的结果如图：

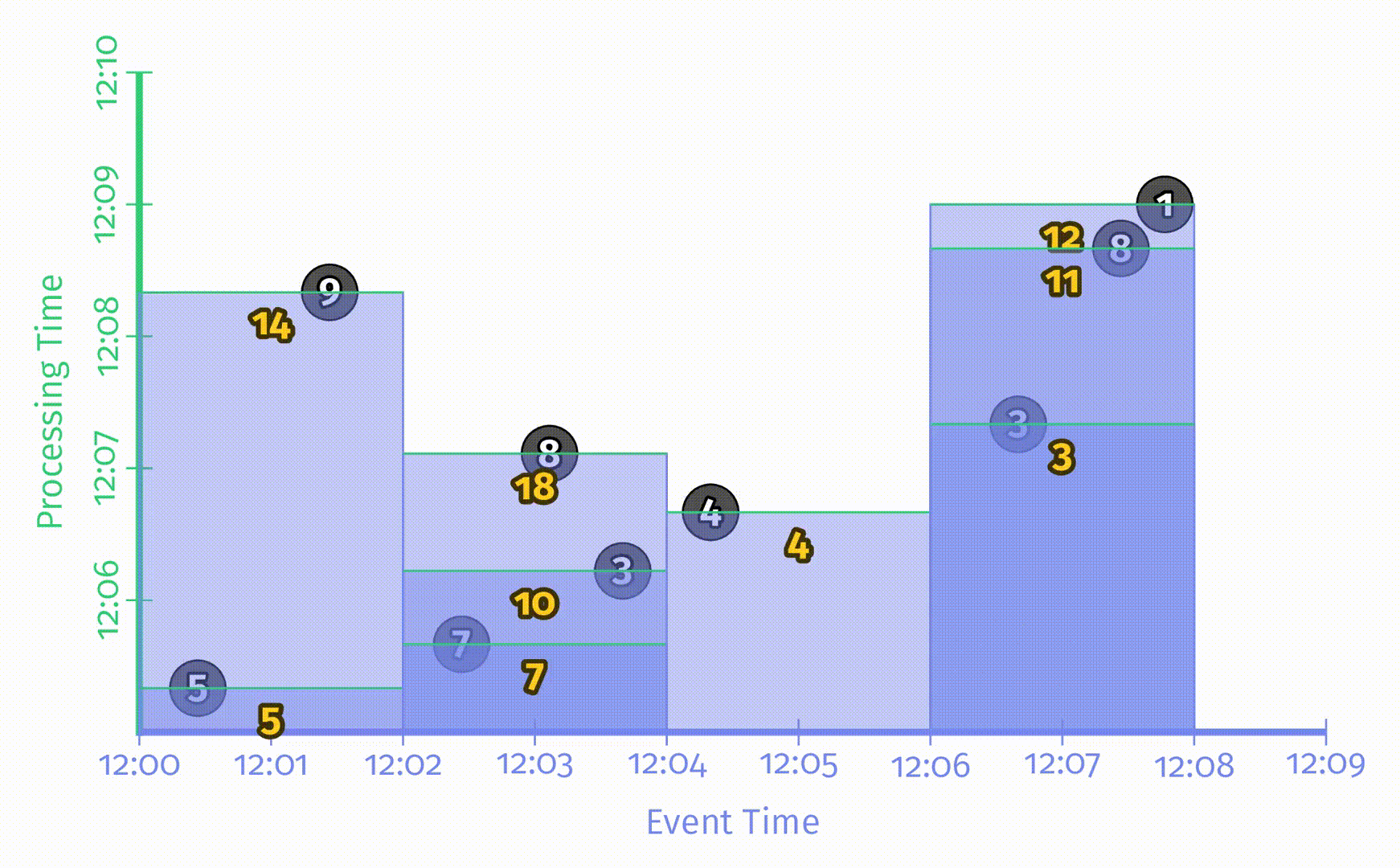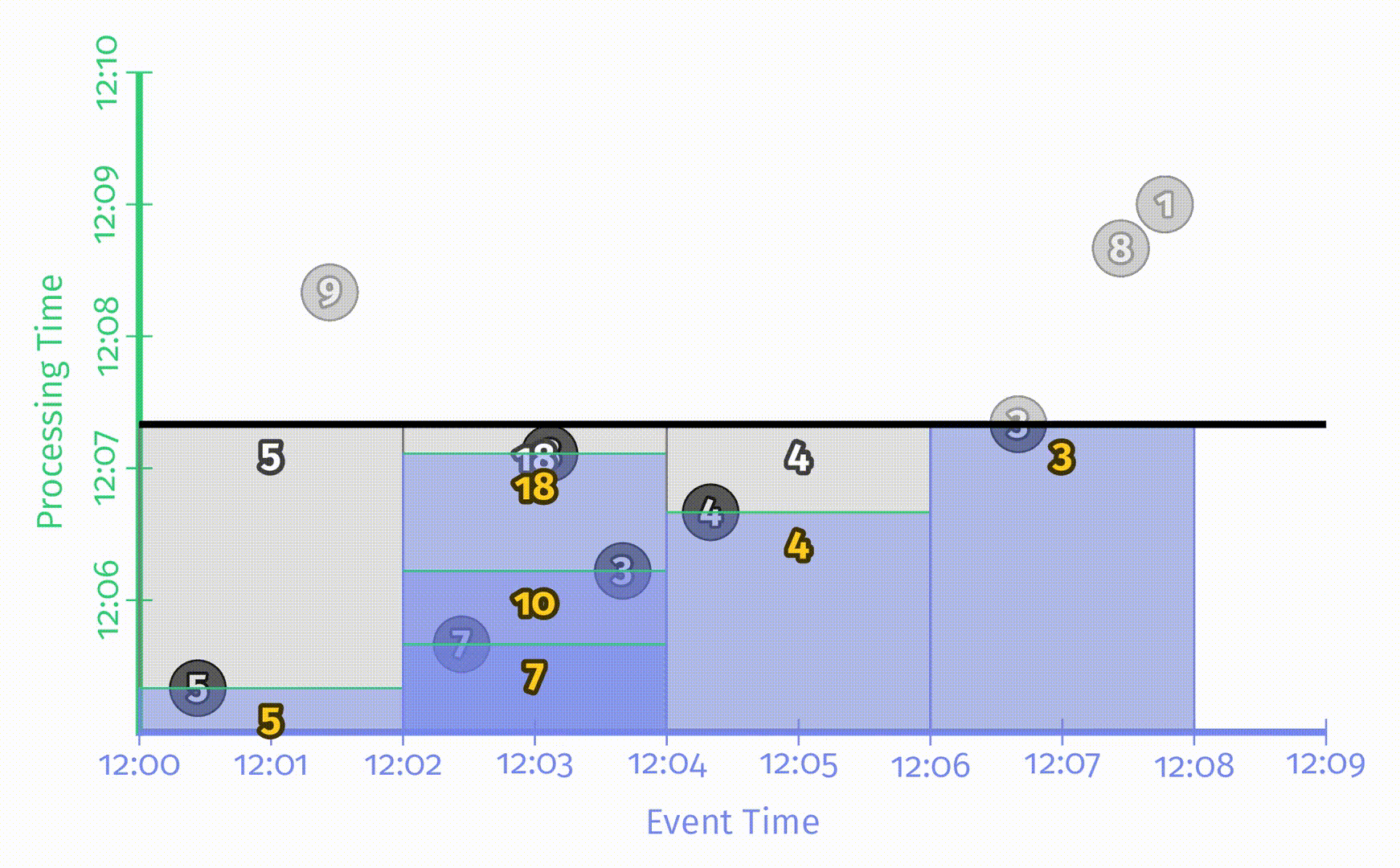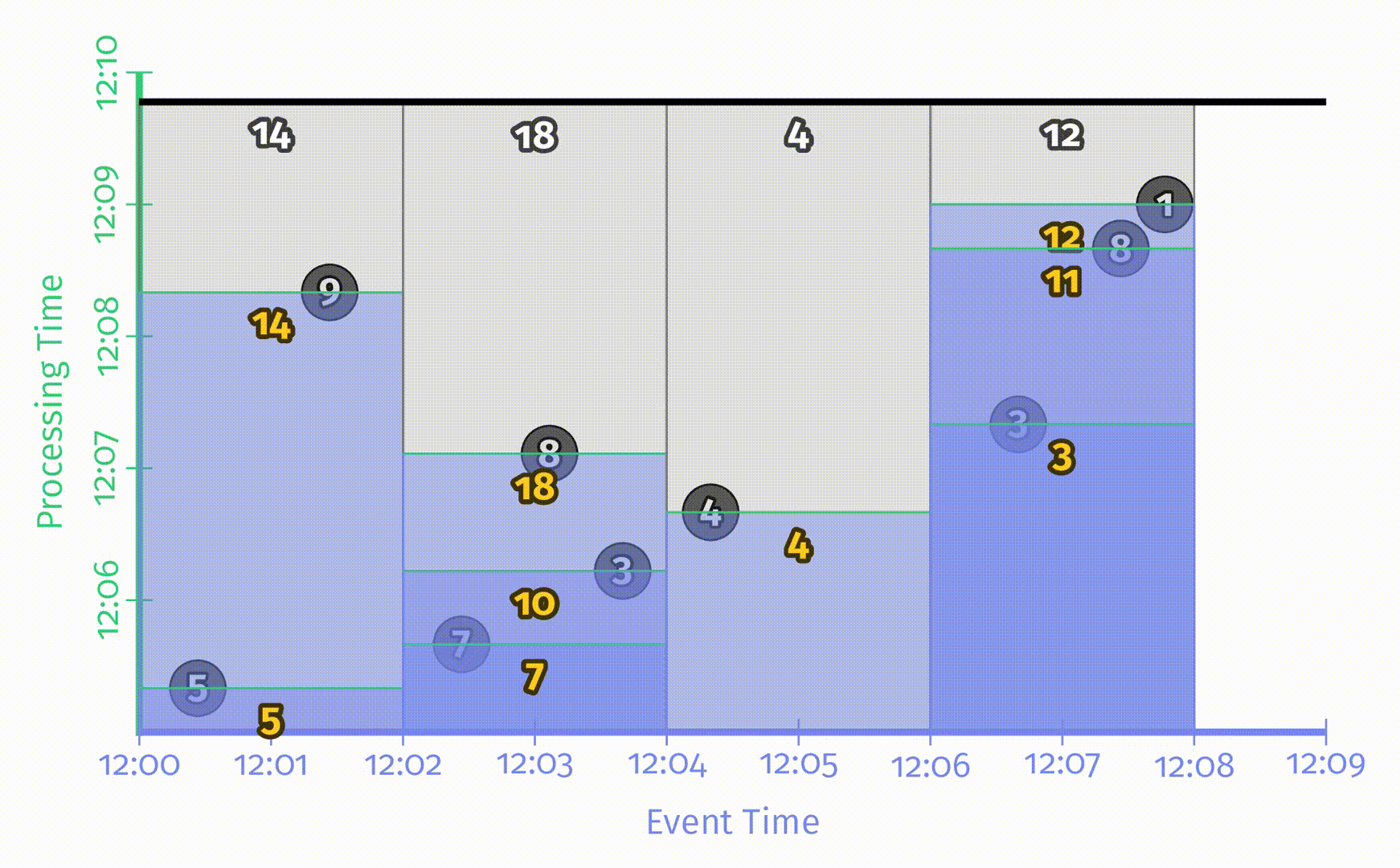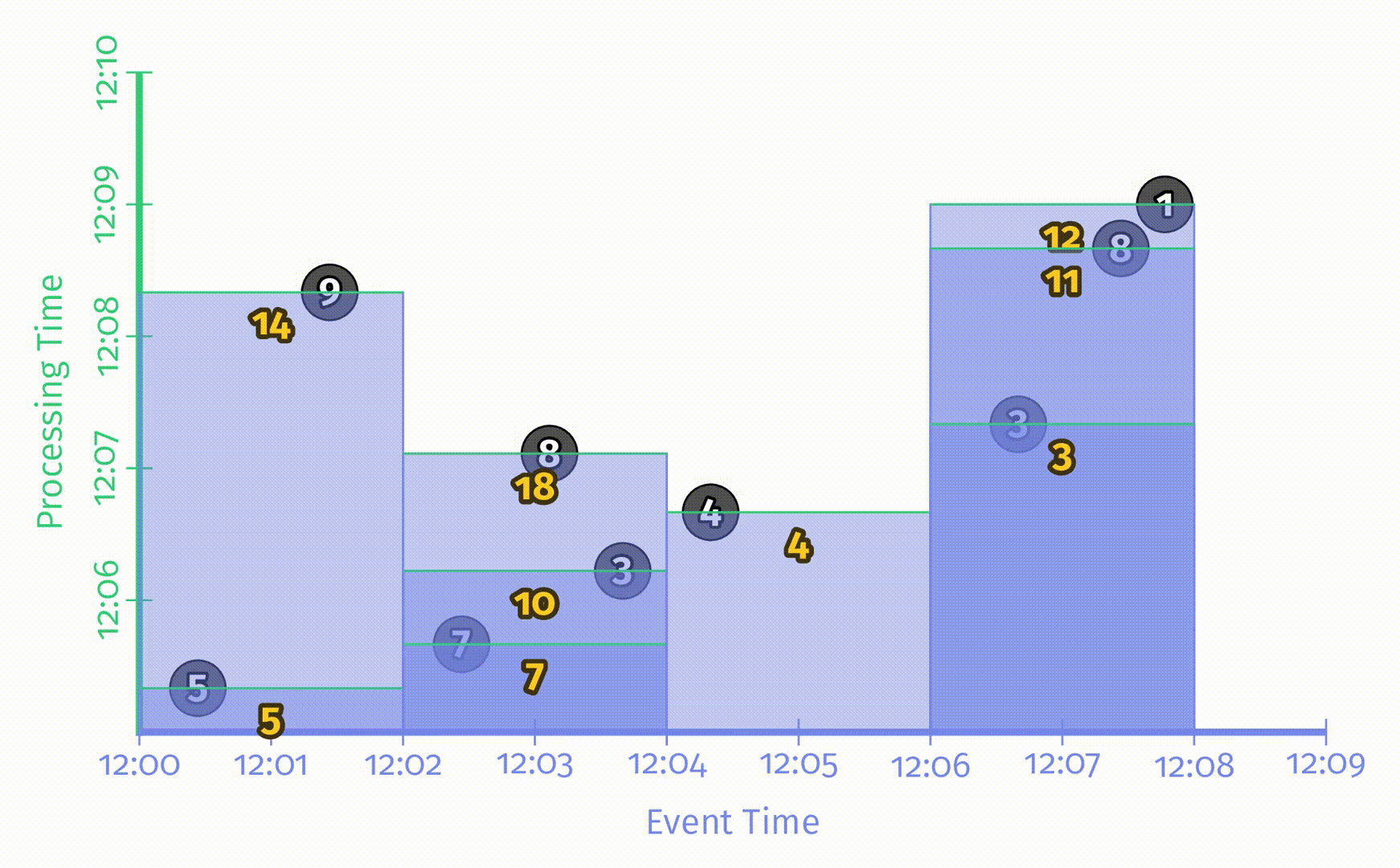
这类触发器在某些场景下工作得很好，比如输出数据流会写入某些经常被用于查询结果的表中，这样的话对于某个给定窗口，在任何时候表中的内容总是最新的，并且这些值会随着时间逐渐收敛为最终的正确值。

但一大缺点在于，针对每条记录的触发器太过于啰嗦。当处理大规模数据时，类似求和之类的聚合可以在不损失信息的情况下有效地降低数据规模，特别是在有大量键值的情况下。此时，你可能更希望在经过一定的处理时间延迟后更新结果，比如每秒或每分钟。使用处理时间延迟的一个好处在于，输出流的数据规模在大量键值之间或不同窗口之间会变得更加统一。

有两种处理时间延迟的触发器设置方法：对齐延迟 和 非对齐延迟。一个对齐延迟的样例如下：

PCollection<KV<Team, Integer>> total = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES))
		.triggering(Repeatedly(AlignedDelay(TWO_MINUTES))))
	.apply(Sum.integersPerKey());

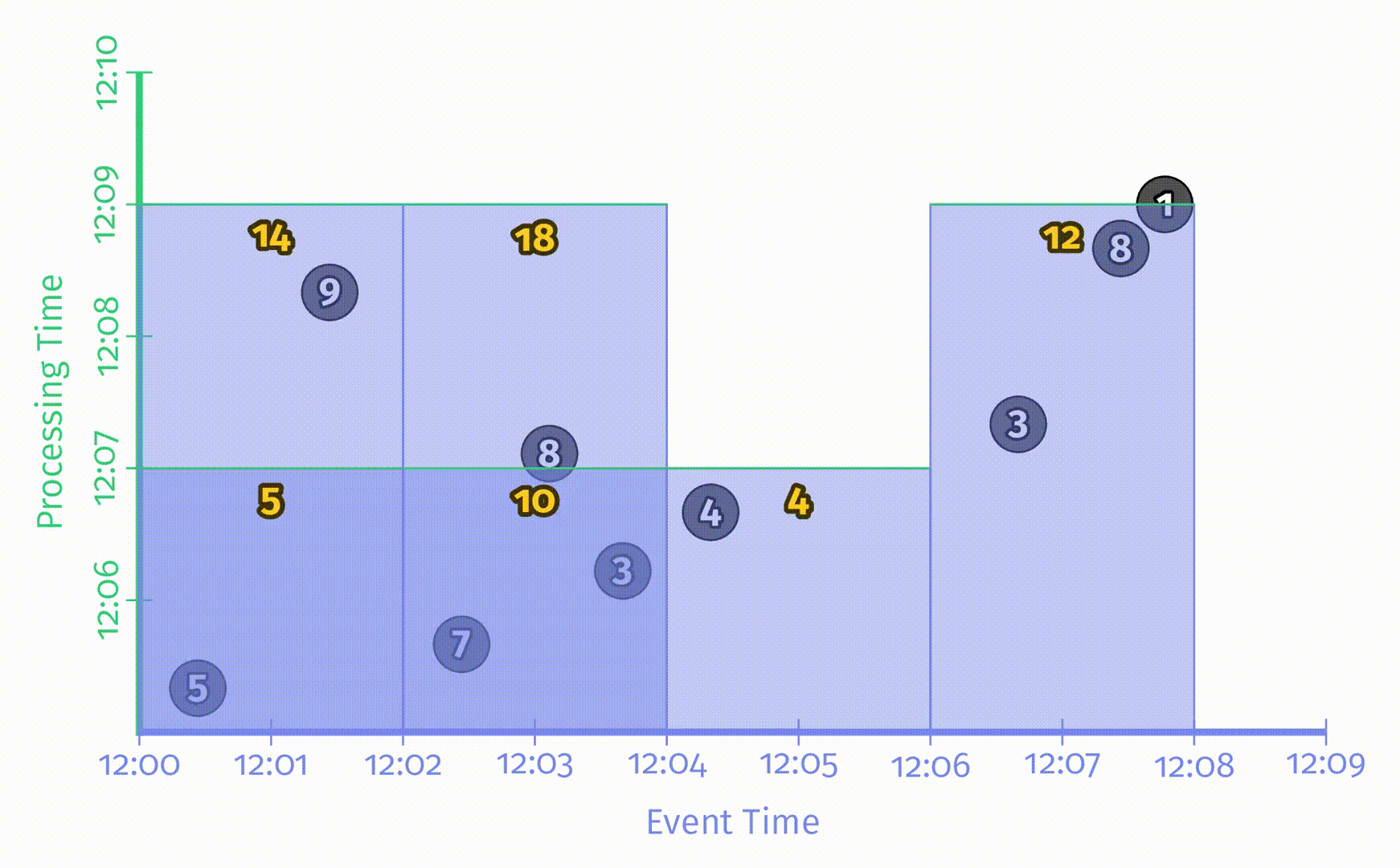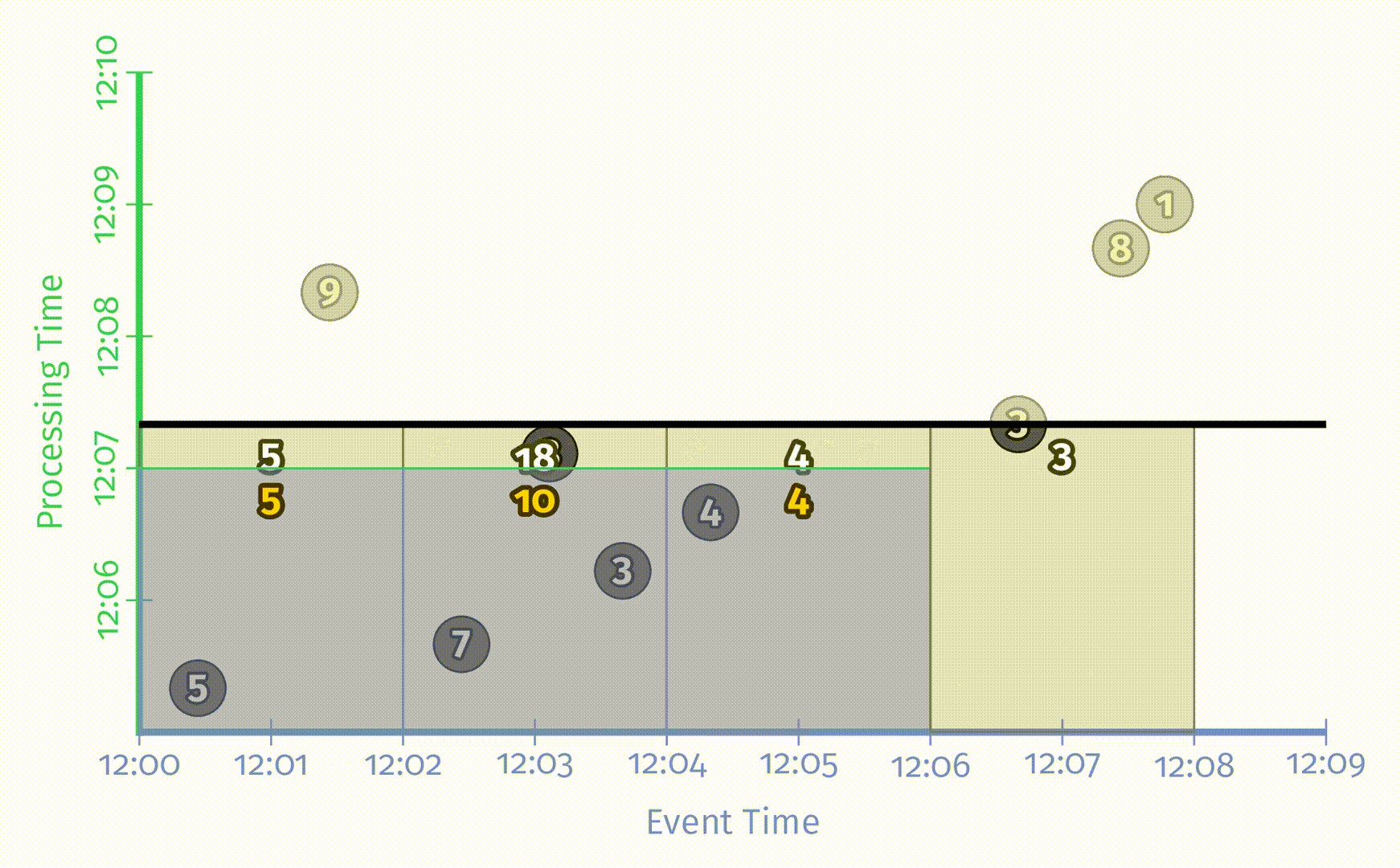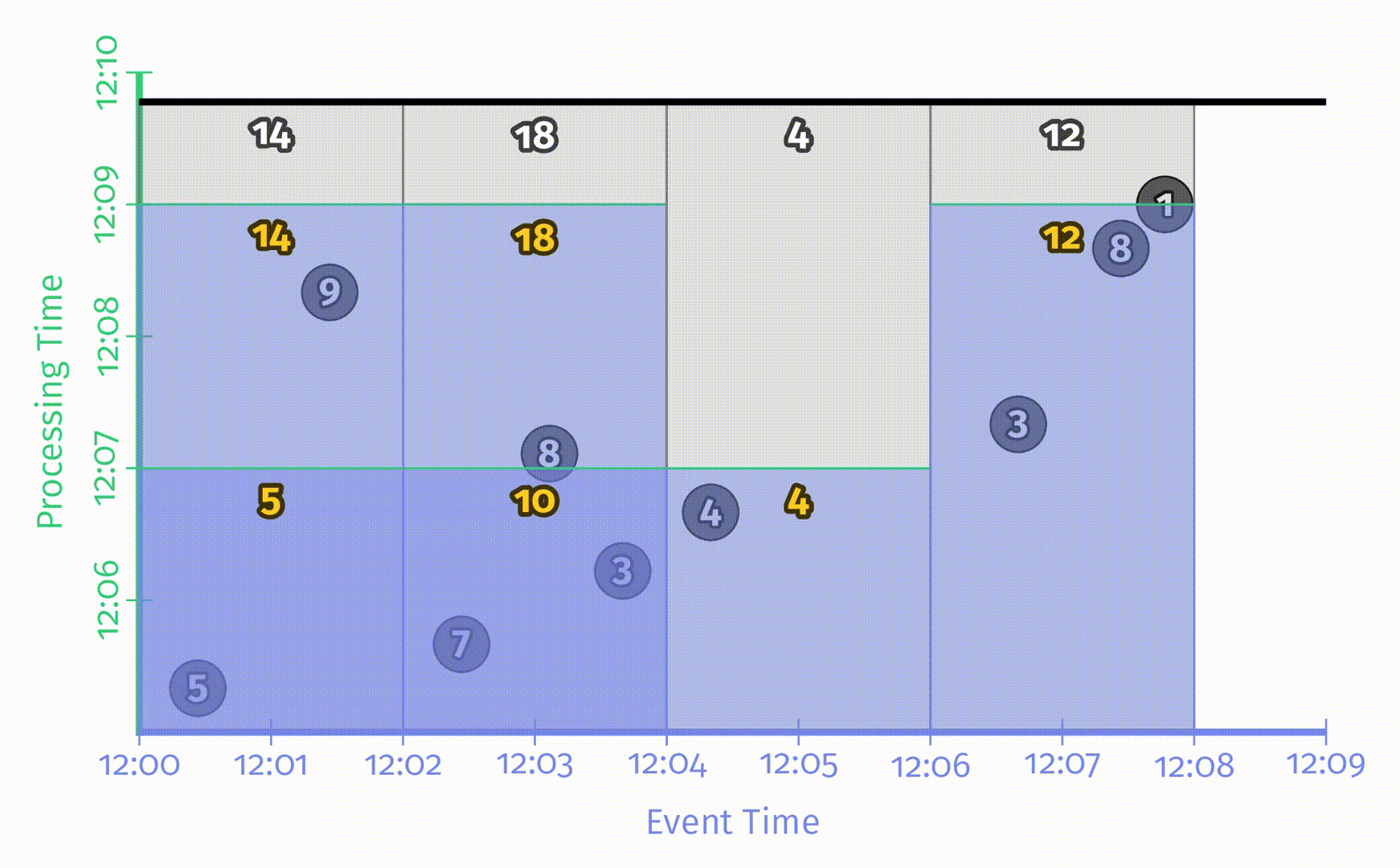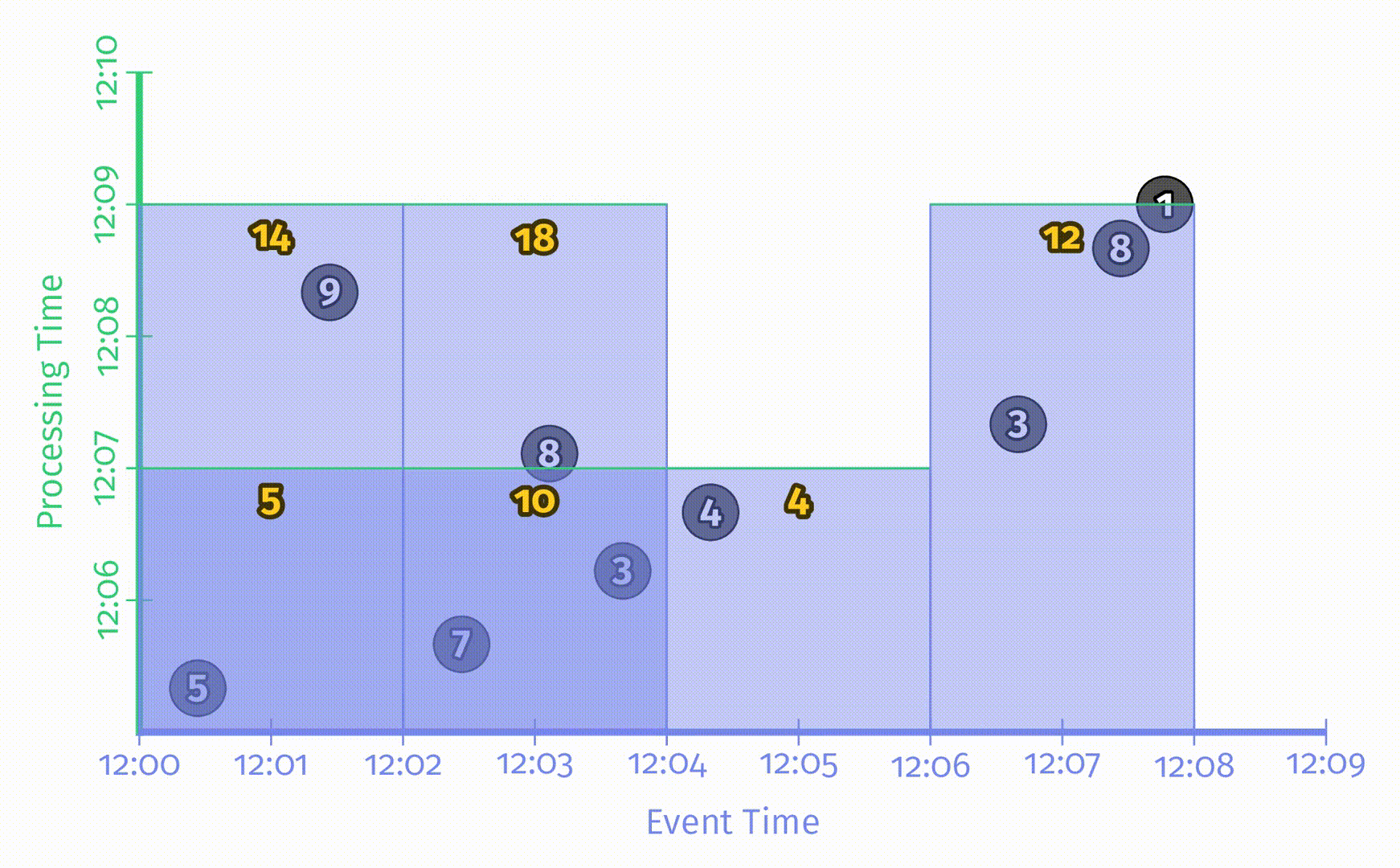
事实上，基于微批处理（microbatch）的系统所提供的便是对齐延迟的触发器，比如 Spark Streaming。它的优点在于可预测性：所有窗口结果都在相同时刻有规律地进行更新，缺点也同样在于此：发生在同一时刻的更新会使得系统负载陡增。对此的解决方法是使用非对齐延迟，样例如下：

PCollection<KV<Team, Integer>> total = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES))
		.triggering(Repeatedly(UnalignedDelay(TWO_MINUTES))))
	.apply(Sum.integersPerKey());

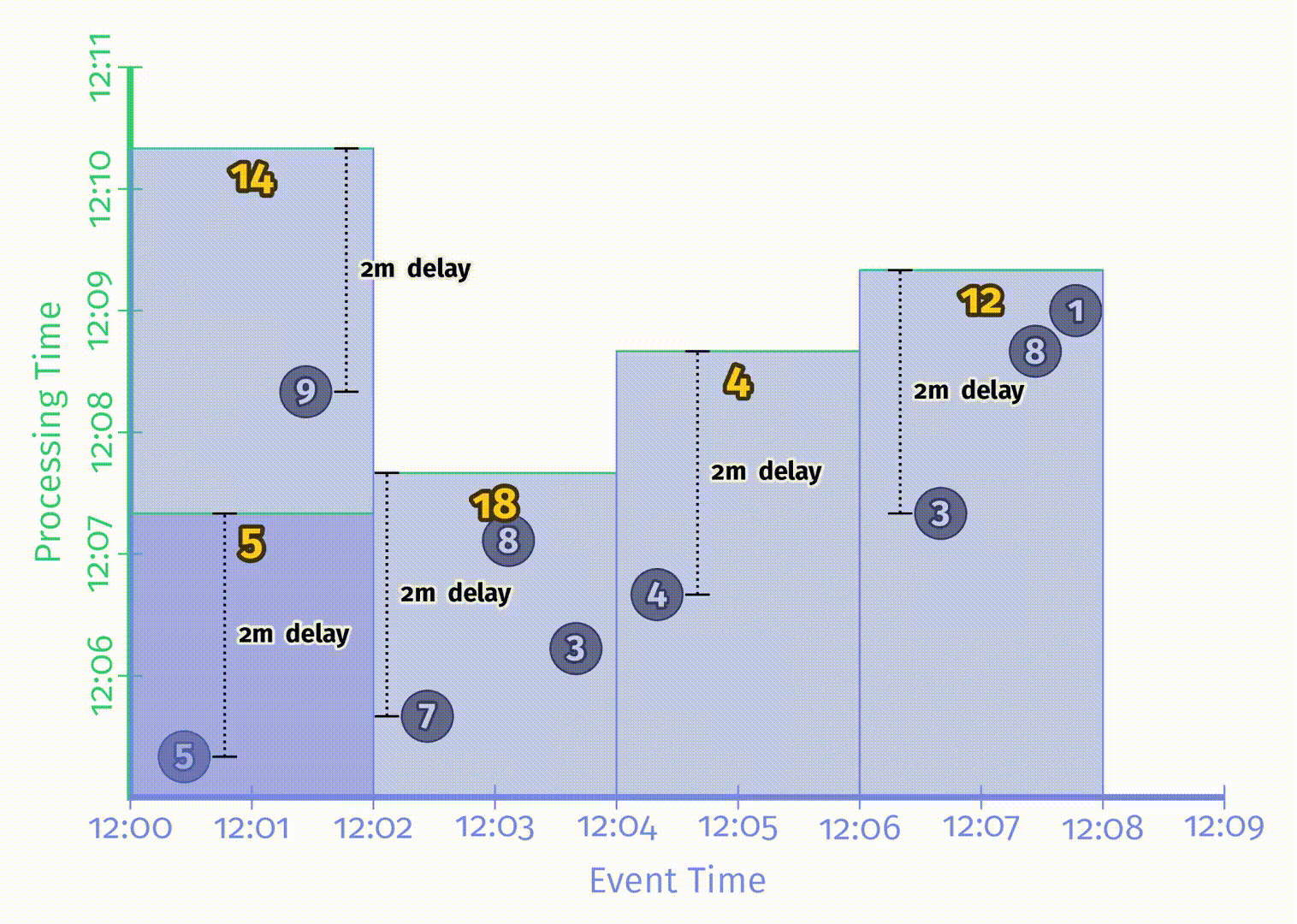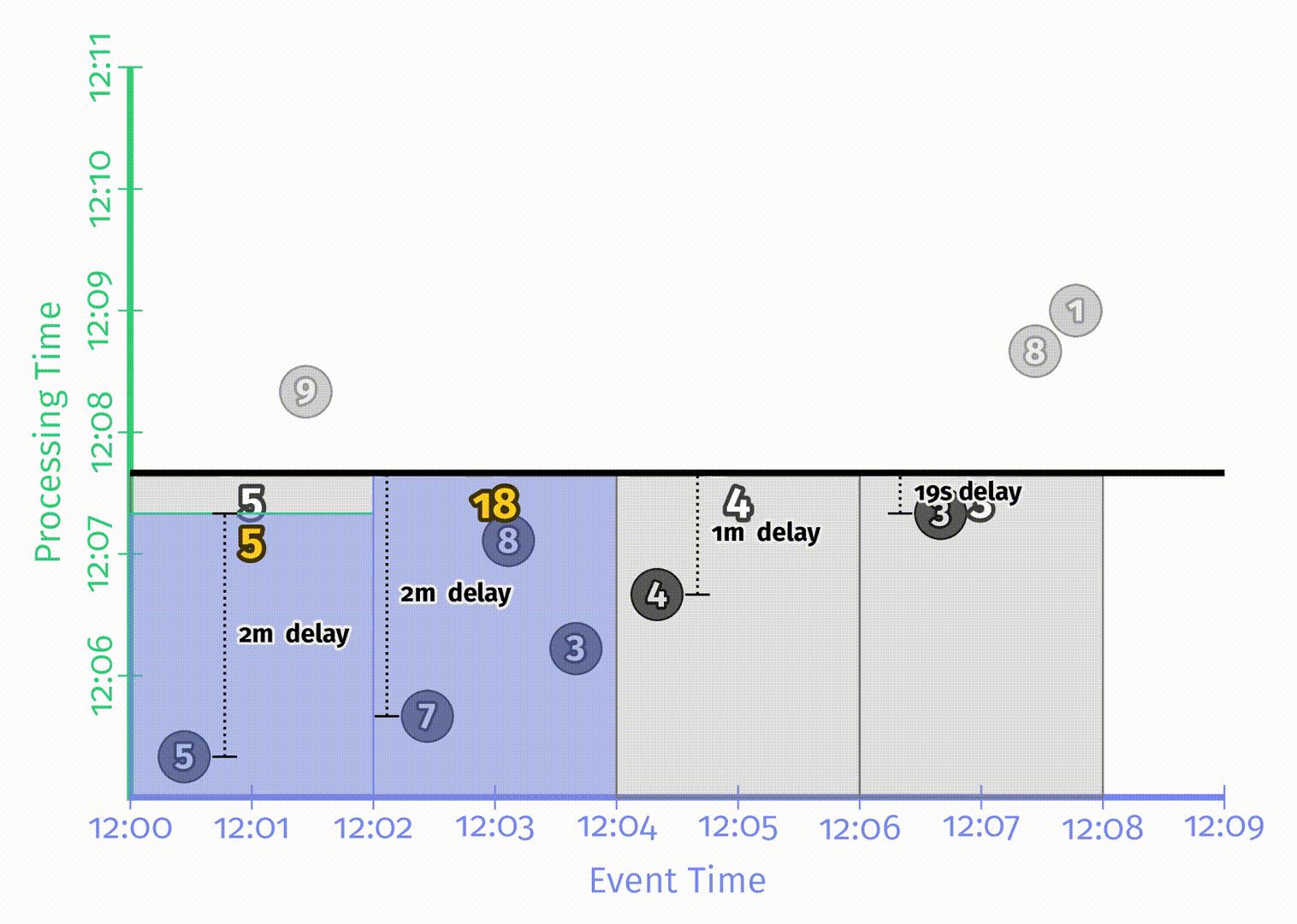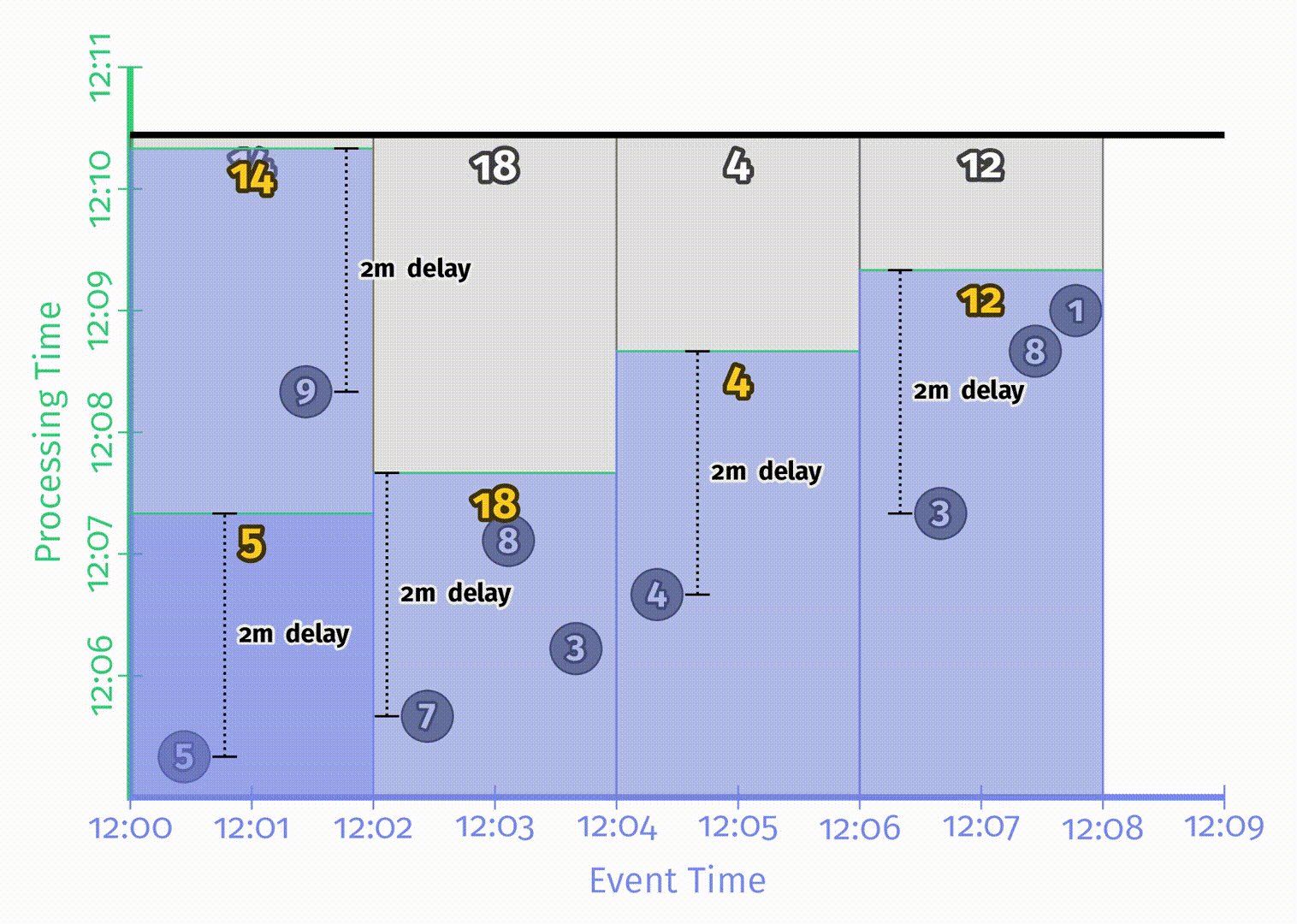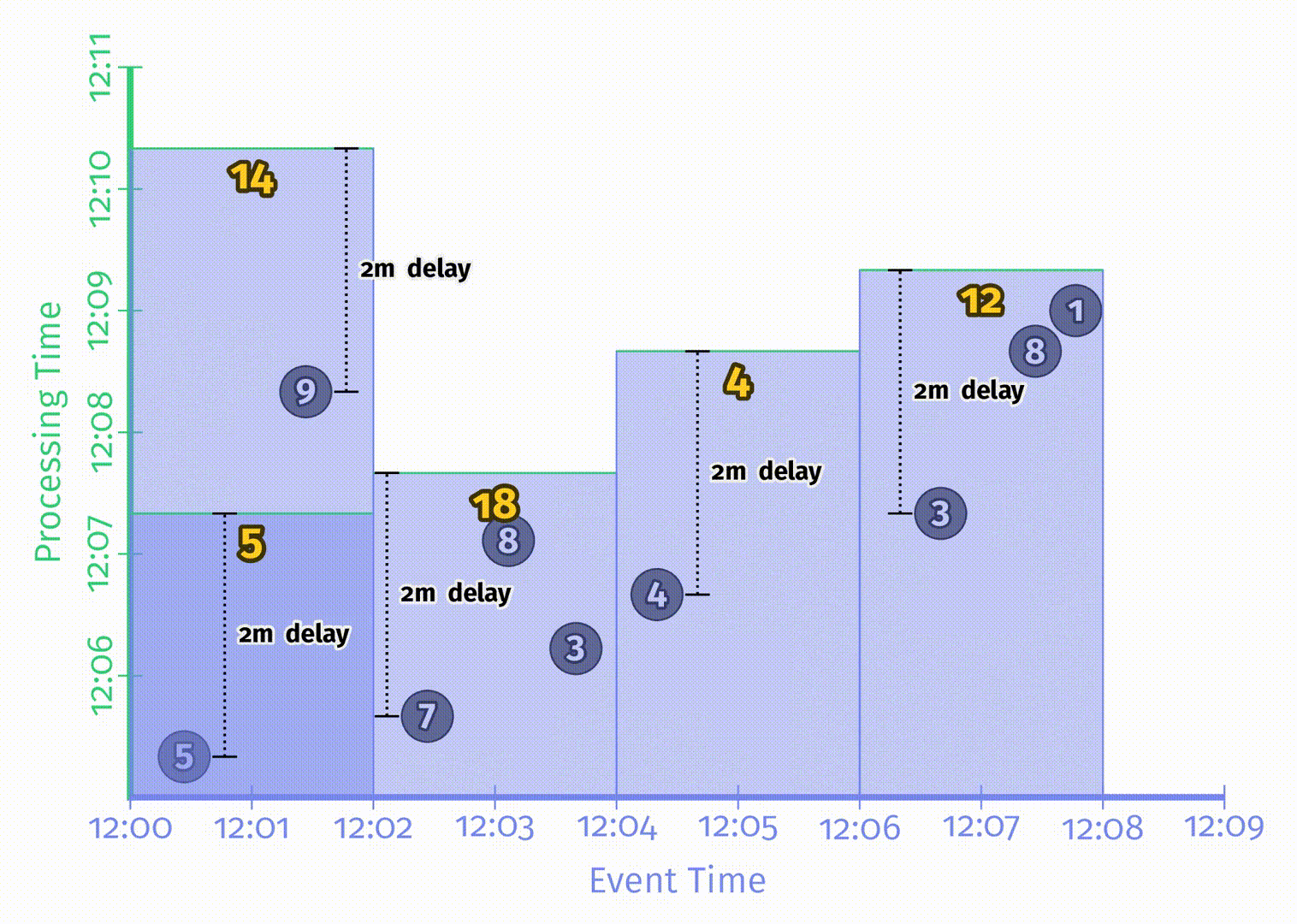
可以看出，非对齐延迟使得负载在时间上的分布更为均匀。

在一些用户场景中，结果可以简单地进行周期性更新，并逐渐趋于正确值，并且我们并不在意何时能保证正确，此时使用重复更新式的触发器是非常合适的。但是在对输入完整性要求比较高的情况下，需要通过一些方法来推断完整性，也就是下一节中的水位线。

When：水位线

水位线是用来回答 When 这个问题答案的一部分。水位线是描述事件时间中输入完整性的时间概念，它是系统用来度量相对于事件流中正在处理的记录的事件时间进度和完整性的方法。

在概念上，可以认为水位线是一个函数，$F(P)\rightarrow E$，输入是处理时间中的某一时刻，返回一个事件时间中的时刻。

更准确地说，函数的输入是在 $P$ 时刻 pipeline 中正在观察水位线的位置其上游的所有状态：输入源、缓存数据、正在处理的数据等等。

系统会认为所有事件时间小于 $E$ 的输入都已经被处理，即断言小于事件时间 $E$ 的数据不会再出现。水位线的类型有两种，对于完美水位线，这样的断言是严格保证的，而对于启发式水位线，这只是一个猜测值。

• 完美水位线
  对于那些我们对所有输入都有完整了解的场景，可以构建出完美的水位线。在这样的场景下，所有数据都会按时到达，不会迟到。
• 启发式水位线
  对于众多分布式输入数据源，我们无法知道输入的完整信息，这种情况下的方法是提供一个启发式水位线。启发式水位线使用任何可获得的信息作为输入，提供一个尽可能准确的猜测。虽然在很多场景下这样的猜测是非常准确的，但是它仍然可能会出现错误，也就是出现迟到数据。之后会提到如何处理迟到数据。

水位线是构成之前提到的完整性触发器的基础。水位线是一个有趣且复杂的话题，在第三章中会深入分析。以下是一个使用水位线构建的完整性触发器的例子：

PCollection<KV<Team, Integer>> totals = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES))
		.triggering(AfterWaterMark()))
	.apply(Sum.integersPerKey());

水位线有趣的地方在于它们是一系列函数，这意味着有多个不同的函数 $F(P)\rightarrow E$ 满足水位线的属性要求。水位线的算法与 pipeline 本身是无关的，在这一章中不会讨论水位线的实现细节。为了对比不同的水位线函数，这里我们在相同的数据集上使用了两种不同的水位线实现，在下图中，左侧是完美水位线，右侧是启发式水位线。在这两个例子中，窗口都是在水位线超出窗口结束时间后产生窗口结果的。

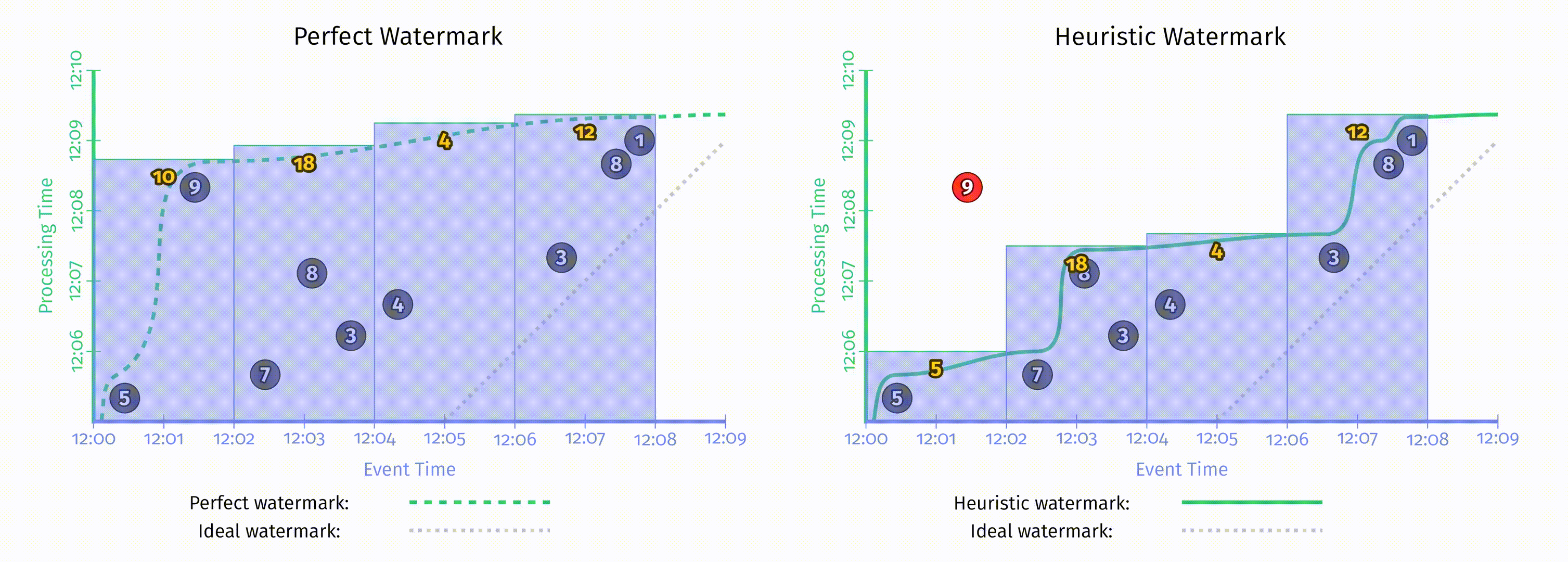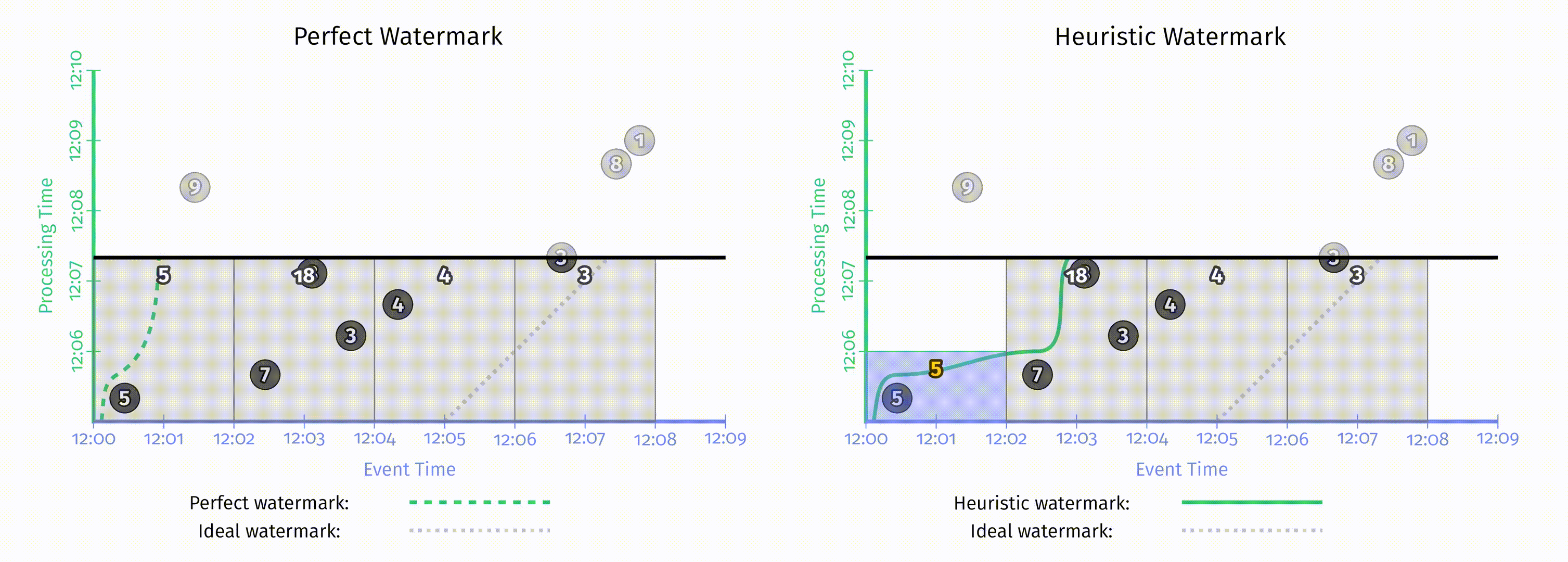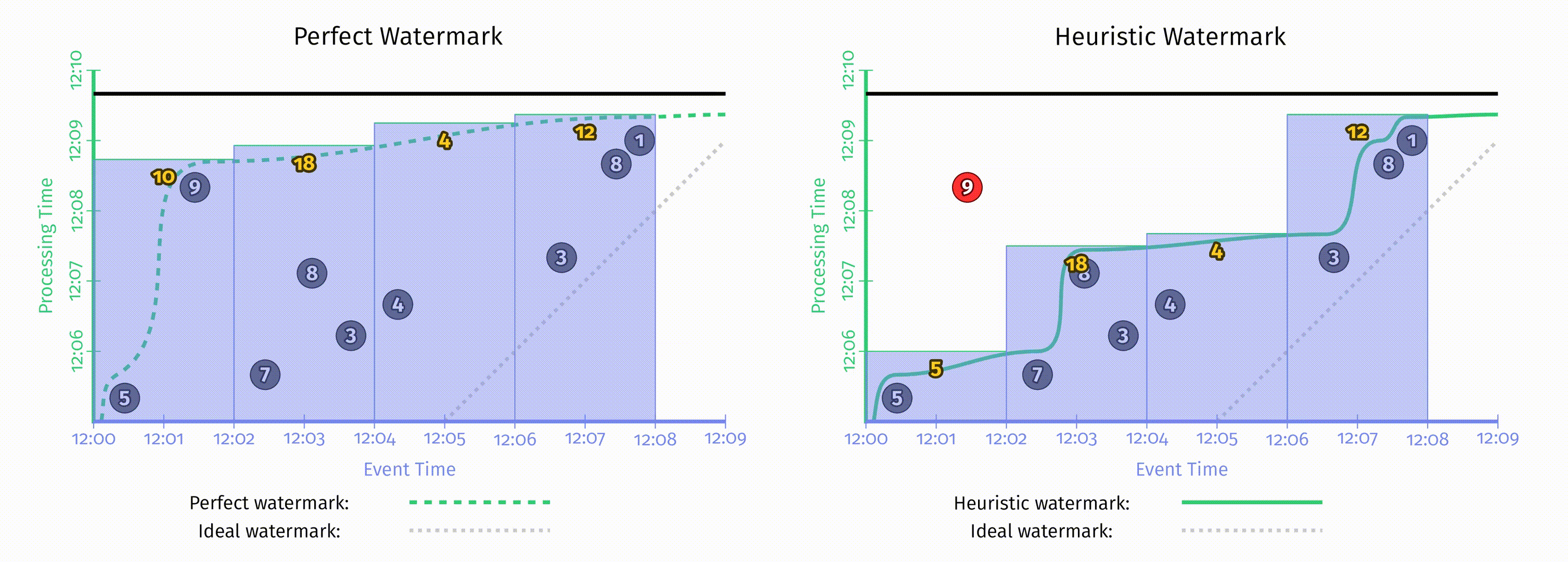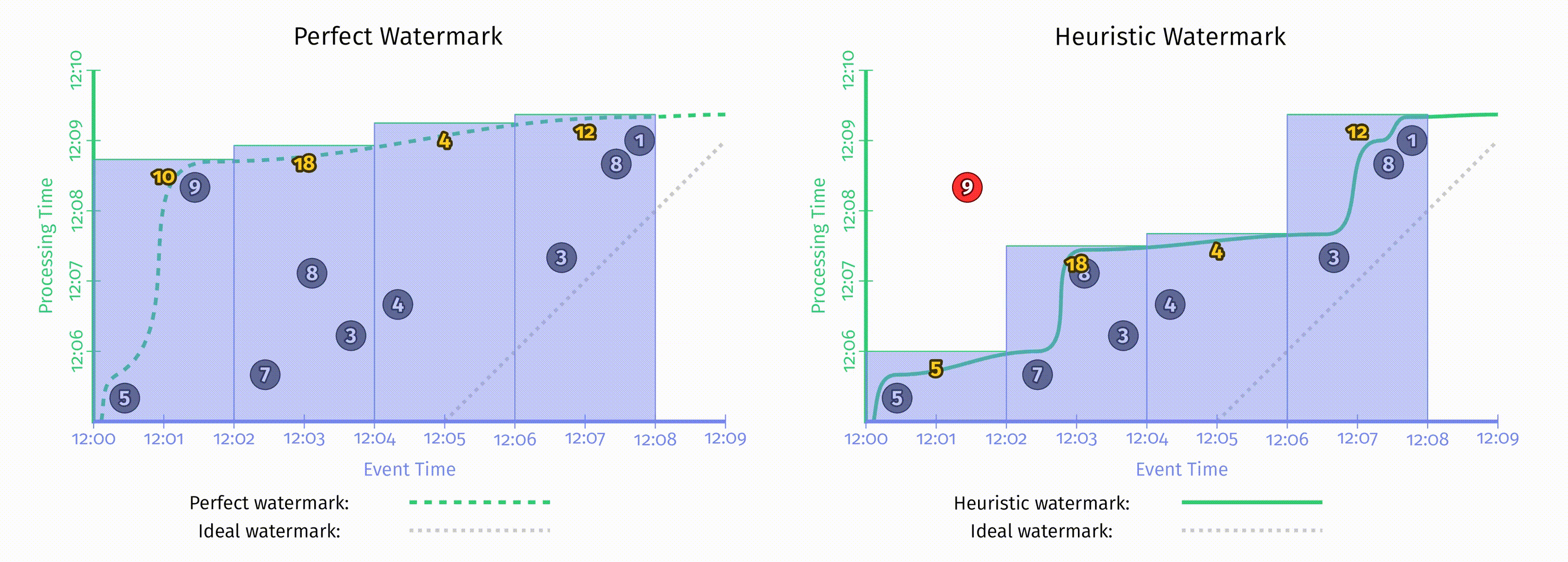
水位线的缺点可能有以下两种：

• 过慢
  当水位线由于一些已知的未被处理数据所推迟时，如果仅仅依赖水位线的推进来产生结果，那么输出结果也会推迟。正如上图左侧 [12:02, 12:04) 的窗口。
  很重要的一点是：尽管水位线提供了非常有用的完整性概念，但从延迟的角度来看，基于完整性来产生输出通常是不理想的。
• 过快
  当启发式水位线推进过快时，事件时间在水位线之前的数据可能会迟到，上图右侧即出现了这一情况，正确结果应该是14，但输出是5。当我们关注正确性时，仅仅依赖水位线来决定何时发出结果是不够的。

水位线的这两个缺点说明了，仅仅依赖完整性的概念是无法使系统同时满足低延迟和正确性的。但如果对这两者都有需求，考虑到重复更新式的触发器可以提供低延迟但不保证正确性的更新，而水位线提供了正确性但延迟可能很高，所以我们其实可以把它们两者的能力结合到一起。

When：Early/On-Time/Late 触发器

两种主要类型的触发器：重复更新式触发器和完整性/水位线触发器，将它们结合到一起可能提供更强大的能力。Beam 意识到了这一点，并提供了一个标准水位线触发器的扩展版，它同时可以支持在水位线前或水位线后重复更新式触发。这就是 Early/On-Time/Late 触发器。它将触发器生成的结果分为三类：

• 若干个（可能为0）提前发出的结果，即使用重复更新式触发器在水位线到达窗口结束时间前周期性地发出结果。这弥补了水位线有时 过慢 的缺点。
• 单个的准时发出的结果，即使用完整性触发器在水位线达到窗口结束时间时发出的结果
• 若干个（可能为0）迟到的结果，即使用另一种重复更新式触发器在水位线超出窗口结束时间且有迟到数据到达后的某一时间发出结果。在使用完美水位线时，这样的结果不会出现。这弥补了水位线有时 过快 的缺点。

在下面样例中，我们将 pipeline 做如下更新：使用1分钟对齐延迟的周期性触发器来产生提前发出的结果，和一个针对每个记录都产生输出的触发器来产生迟到结果。

PCollection<KV<Team, Integer>> totals = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES)))
		.triggering(AfterWatermark()
			.withEarlyFirings(AlignedDelay(ONE_MINUTE))
			.withLateFirings(AfterCount(1)))
	.apply(Sum.integersPerKey());

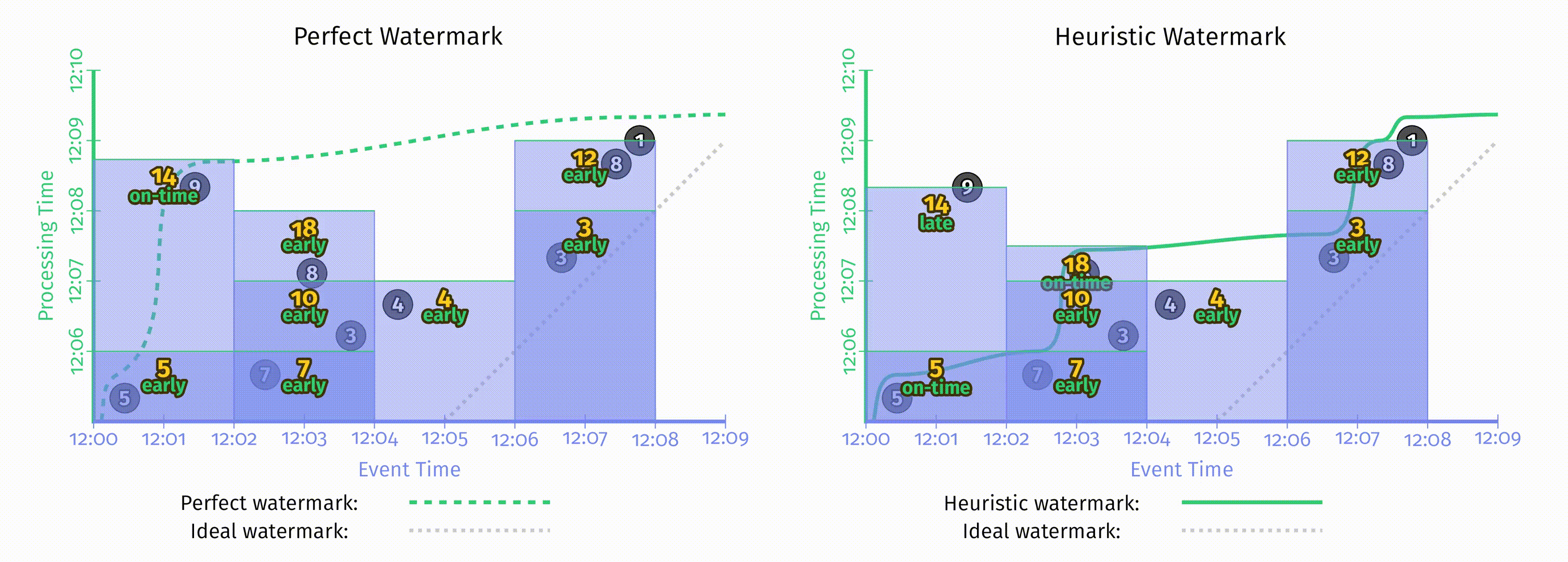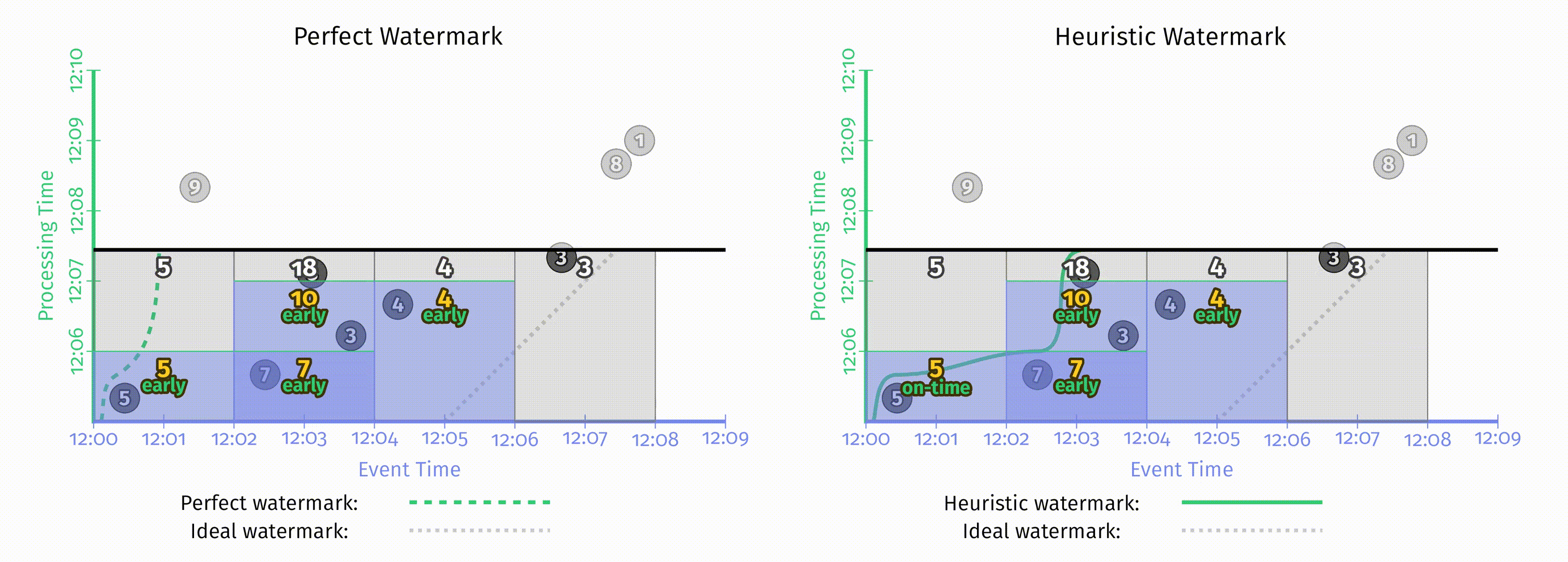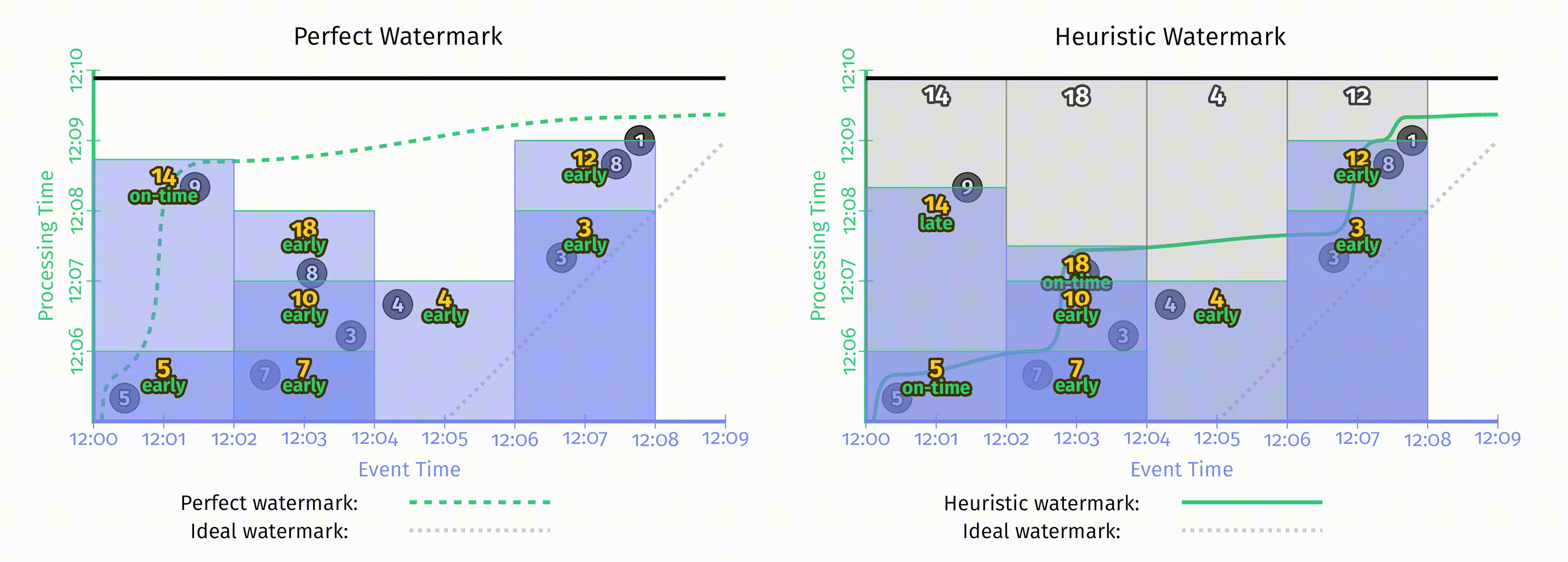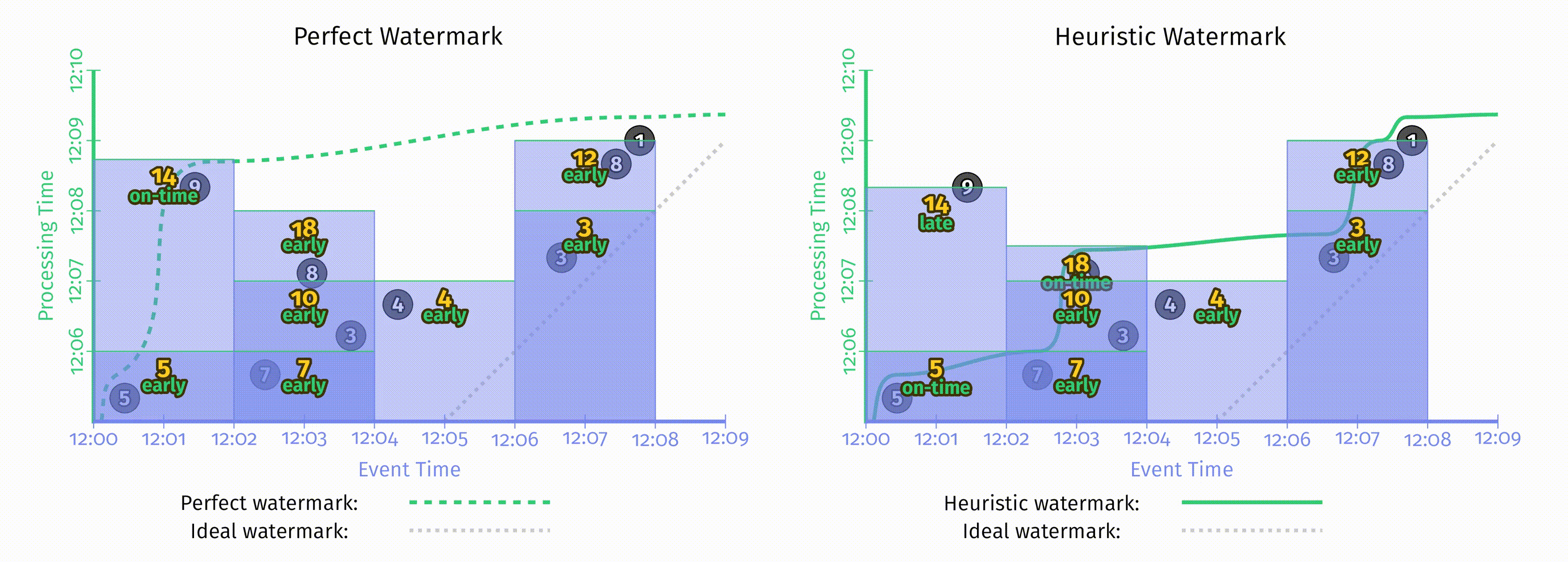
在 Figure 2-10 中，完美水位线与启发式水位线产生的输出看起来非常不同，但使用新的触发器后这两者的输出看起来已经非常相似了。这里的结果与仅仅使用重复触发式触发器看起来也很类似，但因为有了水位线触发器的支持，在这里我们可以推断输入的完整性，从而可以更好地处理关心迟到数据的场景，比如外连接，异常检测等等。

此时的完美水位线与启发式水位线的一大区别在于窗口的生命周期。在完美水位线版本中，我们可以在水位线超出结束时间后立即丢弃该窗口的状态；而在启发式水位线版本中，考虑到可能有迟到数据，我们仍然需要维护窗口状态。但到目前为止，系统并不知道应该将状态维持多久，这是下一节中讨论的内容。

When：允许迟到的限度（垃圾收集）

在 Figure 2-11 中启发式水位线例子里，每个窗口的状态一直持续到样例的整个生命周期，用于处理迟到数据。但在现实中处理无界数据源时，无限制地保留窗口状态是不现实的。系统需要能提供限制窗口生命周期的方法。一个简单的方法是定义一个系统内允许迟到的上界，也就是相对于水位线来说，任意一条记录可能晚到的上界，超出这个晚到限制的数据会被丢弃。当定义了单个数据的迟到上界后，就已经能够准确定义窗口的状态应该维持到什么时候了：即水位线在窗口结束后达到迟到上界的时刻。

在事件时间中指定迟到数据上界可能看上去有点奇怪，但这的确是最好的方法。另一个可选的方法是在处理时间中指定上界（比如在水位线经过窗口结束时间后，在处理时间中再保留十分钟）。但后者可能使 pipeline 中的垃圾收集策略出现问题，比如 worker 宕机导致 pipeline 中断了几分钟，这会导致窗口无法处理本应该能够处理的迟到数据。通过在事件时间中指定延迟上界，垃圾收集可以与 pipeline 真实的处理过程绑定，这样可以降低窗口无法正确处理迟到数据的可能性。
另外，并不是所有的水位线都是一样的，本书中提到的水位线都是 低水位线，它会悲观地去跟踪系统中未被处理的事件时间最早的数据。用低水位线处理迟到数据的好处是可以适应不断变化的事件时间偏差，提供尽可能最好的正确性保证。
作为对比，某些系统可能用“水位线”表示其他事物。比如 Spark Streaming 中的水位线是高水位线，它会乐观地获取系统中事件时间最新的数据。在处理迟到数据时，高水位线会与用户所指定的阈值计算出一个时间值，系统可回收任何早于该值的窗口。换句话说，系统允许你指定在你的 pipeline 中事件时间的偏差上界。这样做在偏差可以保持在某个固定常数的 pipeline 中可以工作地很好，但相比低水位线模式可能更容易错误地丢失数据。

以启发式水位线为例，在 Figure 2-11 的基础上增加1分钟的迟到上界：

PCollection<KV<Team, Integer>> totals = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES)))
		.triggering(AfterWatermark()
			.withEarlyFirings(AlignedDelay(ONE_MINUTE))
			.withLateFirings(AfterCount(1))
		.withAllowedLateness(ONE_MINUTE))
	.apply(Sum.integersPerKey());

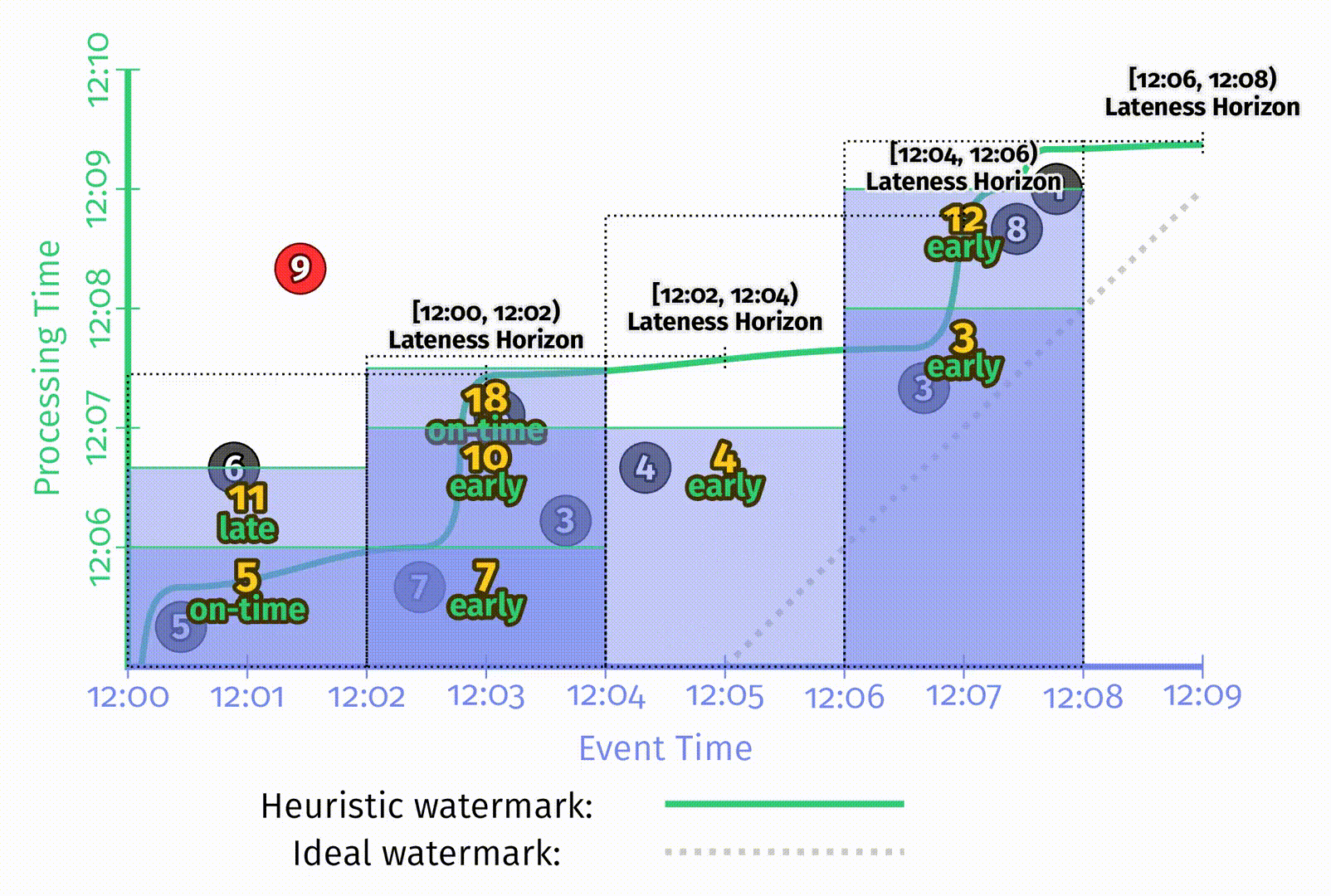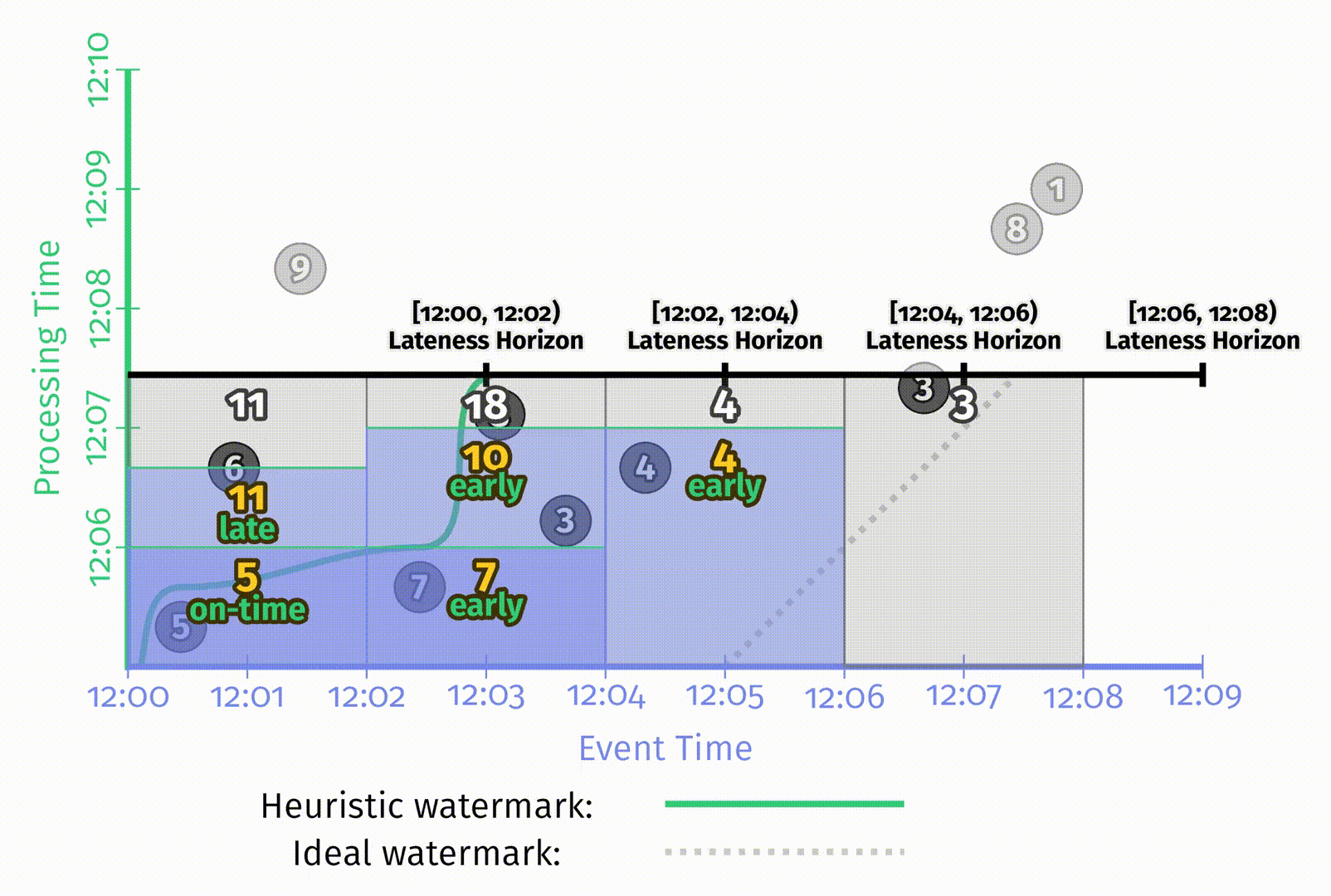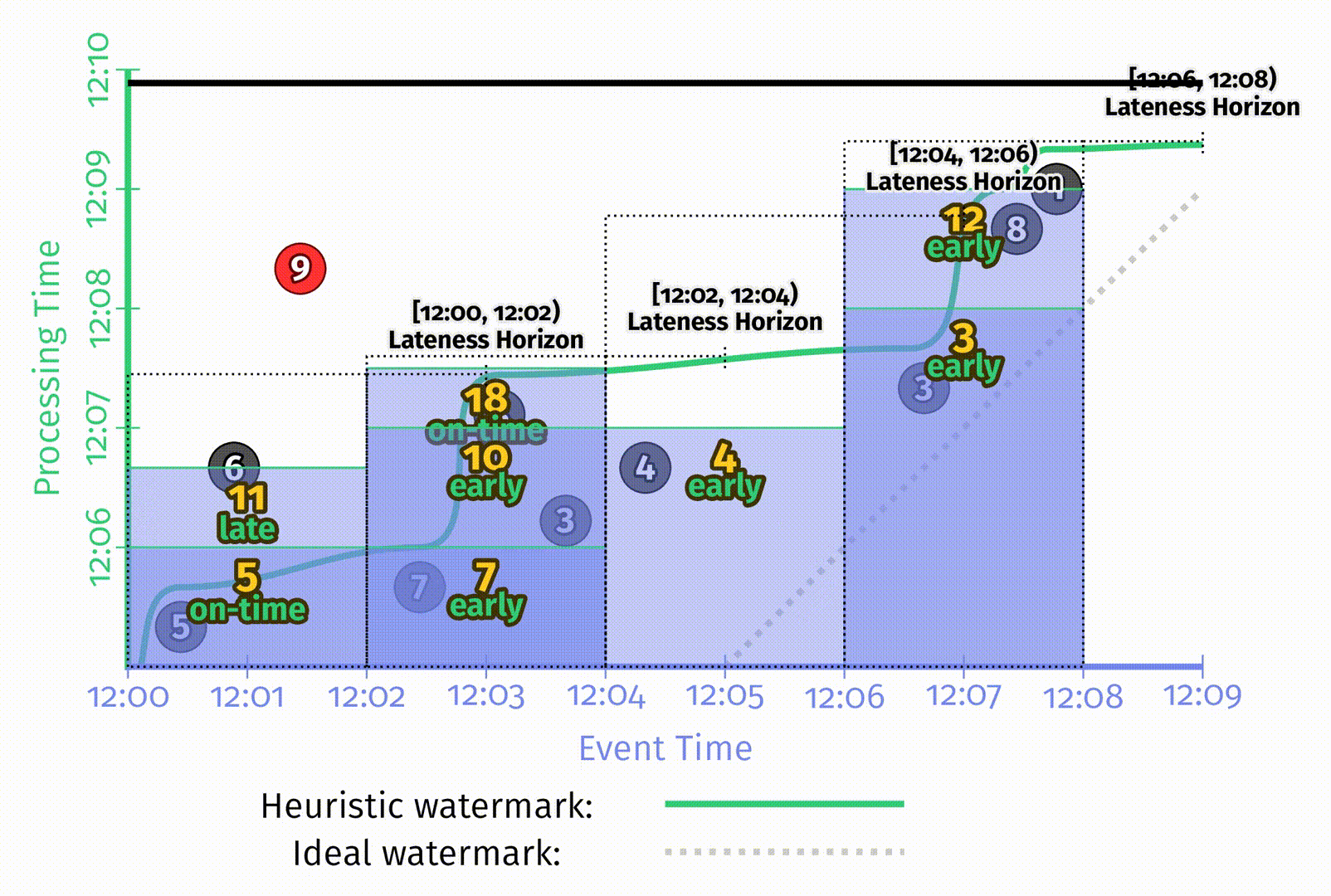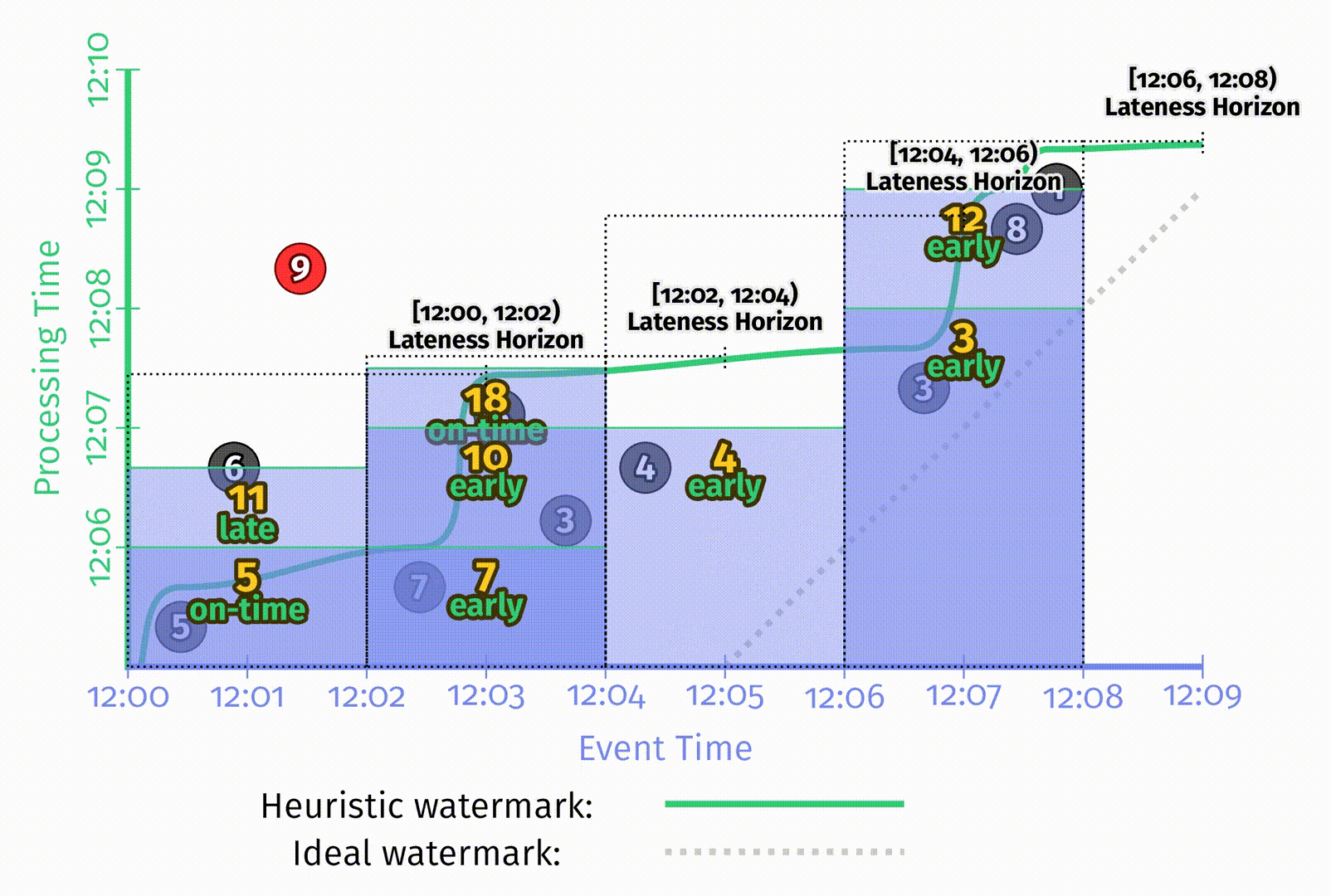
在上图中，为了体现允许迟到带来的影响，添加了如下一些特征：

• 表示当前处理时间位置的黑色粗线上为每个窗口添加了在事件时间中迟到上界的标注。
• 当水位线超出窗口迟到上界时，该窗口会被关闭，即窗口所有的状态会被丢弃。在图中使用了虚线的矩形来表示窗口被关闭时所囊括的时间，虚线矩形右侧的尾巴表示窗口的迟到上界。
• 在这张图中，为第一个窗口额外增加了一条数据6。6是迟到数据，但在迟到上界之内，因此可以被包含到更新后的结果11中。但9在迟到上界后达到，所以被丢弃了。

关于迟到上界的最后两条旁注：

• 对于可以实现完美水位线的情况，不需要处理迟到数据，因此可以将迟到上界设为0。
• 当计算全时间段上的全局聚合，且键值数量很有限时，活动中窗口的数量不会超过键值的数量，只要键值数量是可控的，就不需要通过允许延迟的方式来限制窗口的生命周期。（比如根据不同浏览器类型分组，计算从网站出现以来它们各自访问的总次数）

How：聚合

当触发器会为某个窗口发出多个结果时，就会遇到 How 这个问题：多个结果之间的关系是怎么样的？关于结果的聚合有三种不同的模式：

• 丢弃（Discarding）
  当输出结果被发出后，存储的状态被立即丢弃。这意味着后续的结果与之前的结果之间是独立的。丢弃的模式在下游消费者可以自行进行聚合的场景下是很有用的。
• 累积（Accumulating）
  当输出结果被发出的，状态依然保持，未来的输入会聚合到当前状态中。累积模式对于后续结果可以简单地覆盖之前结果的场景是很有用的。
• 累积并撤销（Accumulating and retracting）
  与累积模式很类似，但在产生一个新的结果时，同样会为之前的某个或多个结果产生一个撤销。这就像是在说：”我之前告诉你的结果 X 是不对的，丢弃掉 X 这个结果，把它改成 Y“。在下面两种场景下，撤销是非常有用的：
  • 当下游消费者需要在不同的维度上对数据重新分组时，新的值可能导致数据被分到不同的组中。这时不能简单地覆盖旧的结果，而需要用撤销来移除旧的值
  • 当使用动态窗口（如会话）时，因为会发生窗口合并，所以新值出现可能会替换掉多个旧的窗口。

下面的例子展示了丢弃模式：

PCollection<KV<Team, Integer>> totals = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES)))
		.triggering(AfterWatermark()
			.withEarlyFirings(AlignedDelay(ONE_MINUTE))
			.withLateFirings(AfterCount(1))
		.discardingFiredPanes())
	.apply(Sum.integersPerKey());

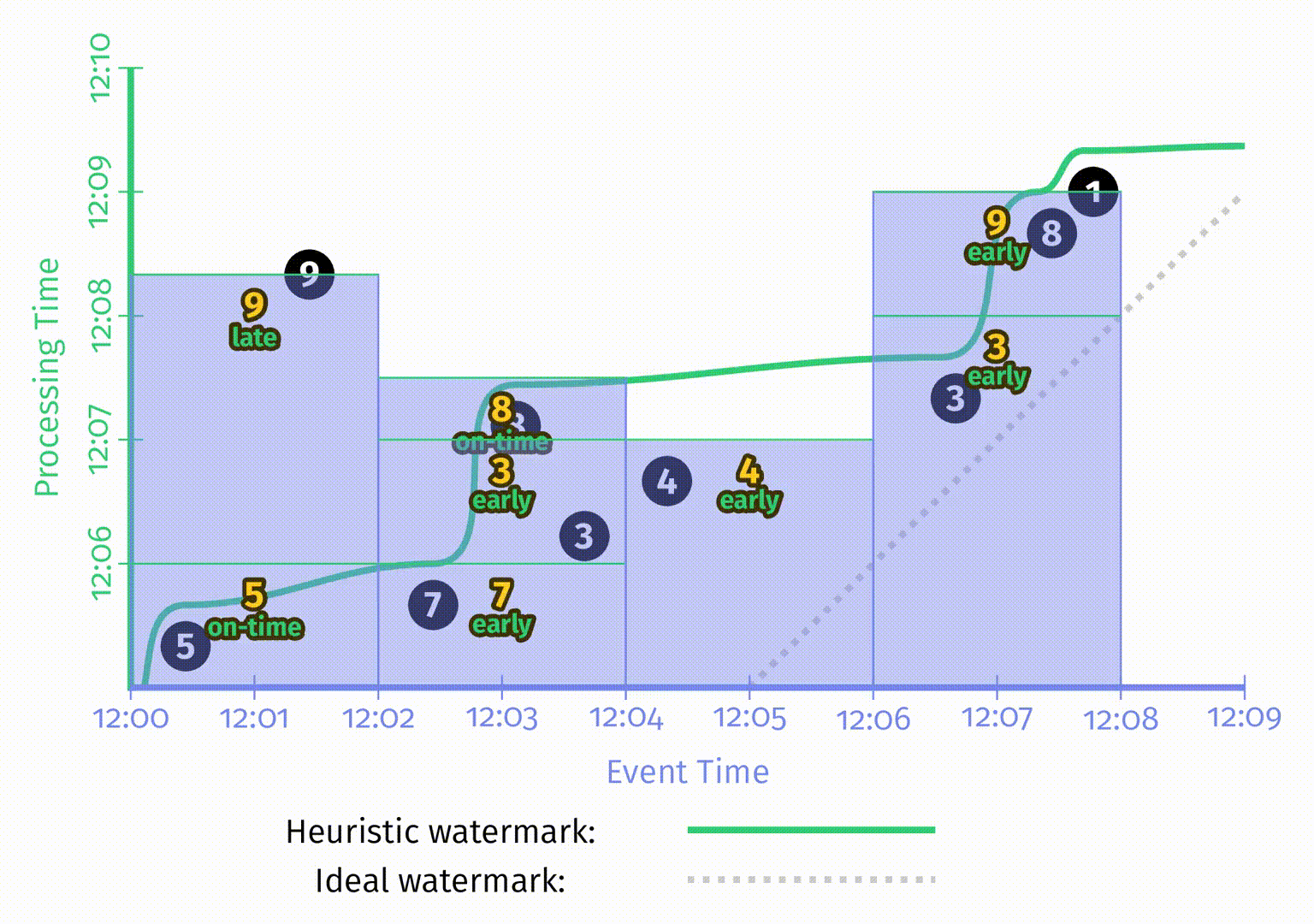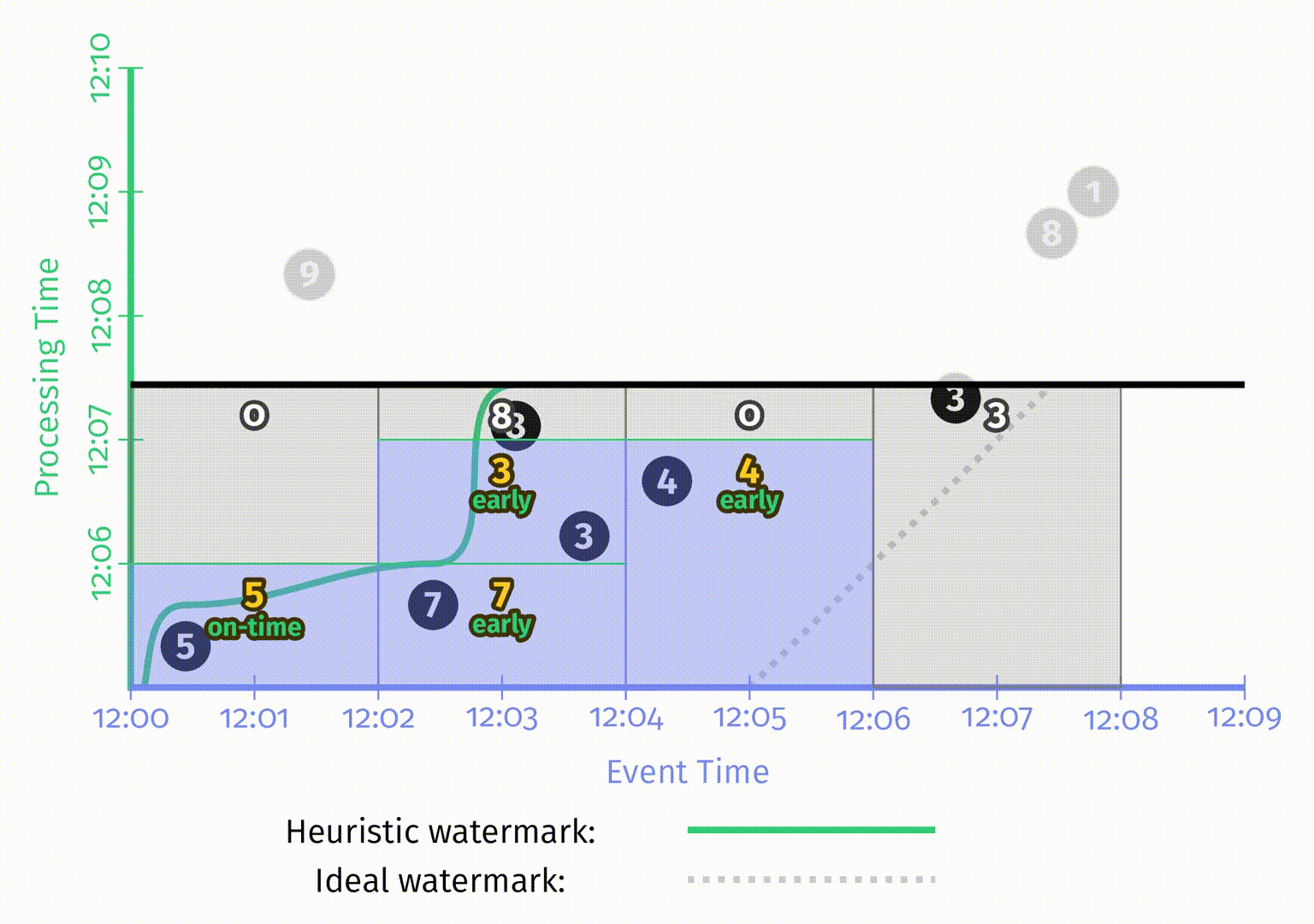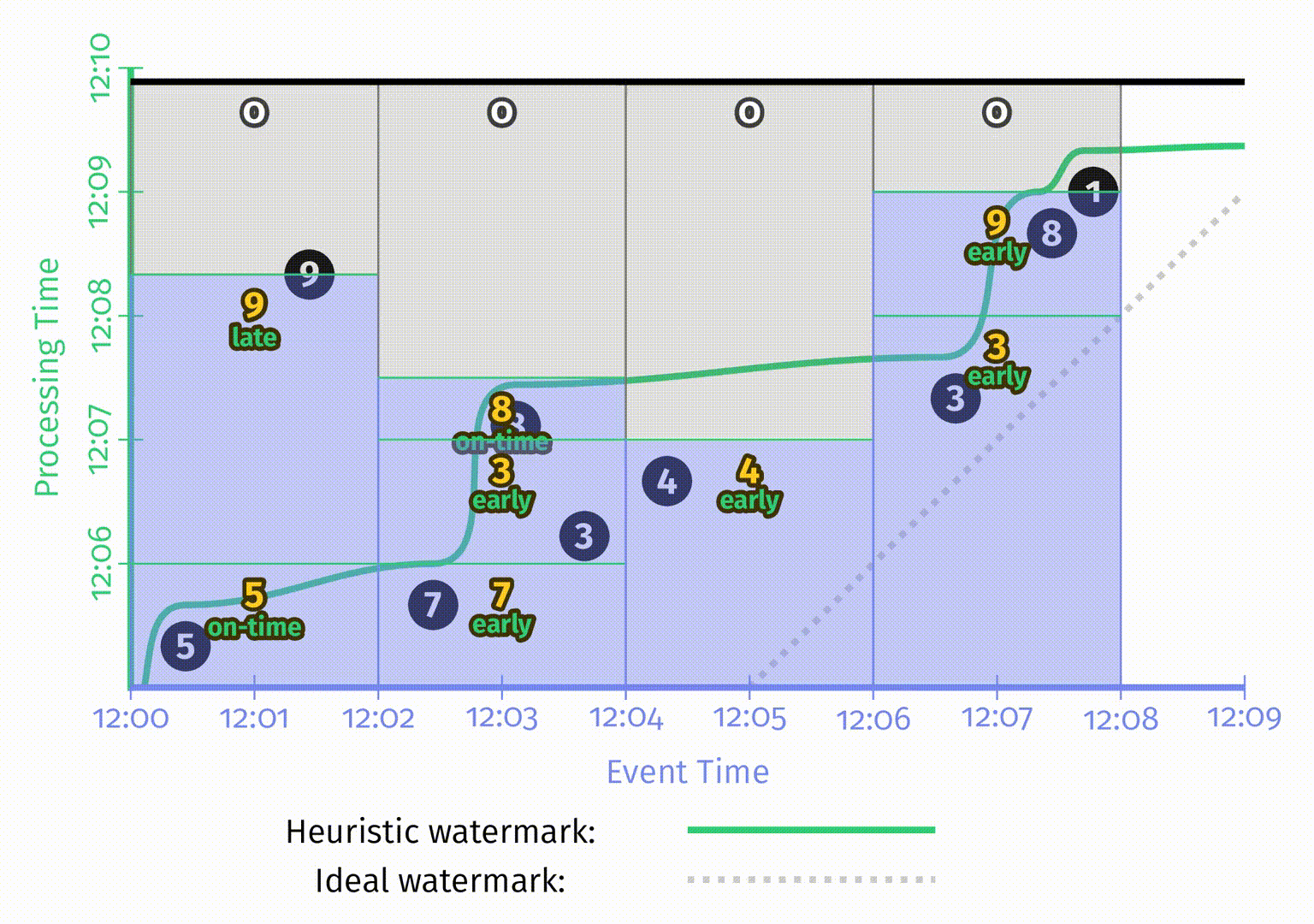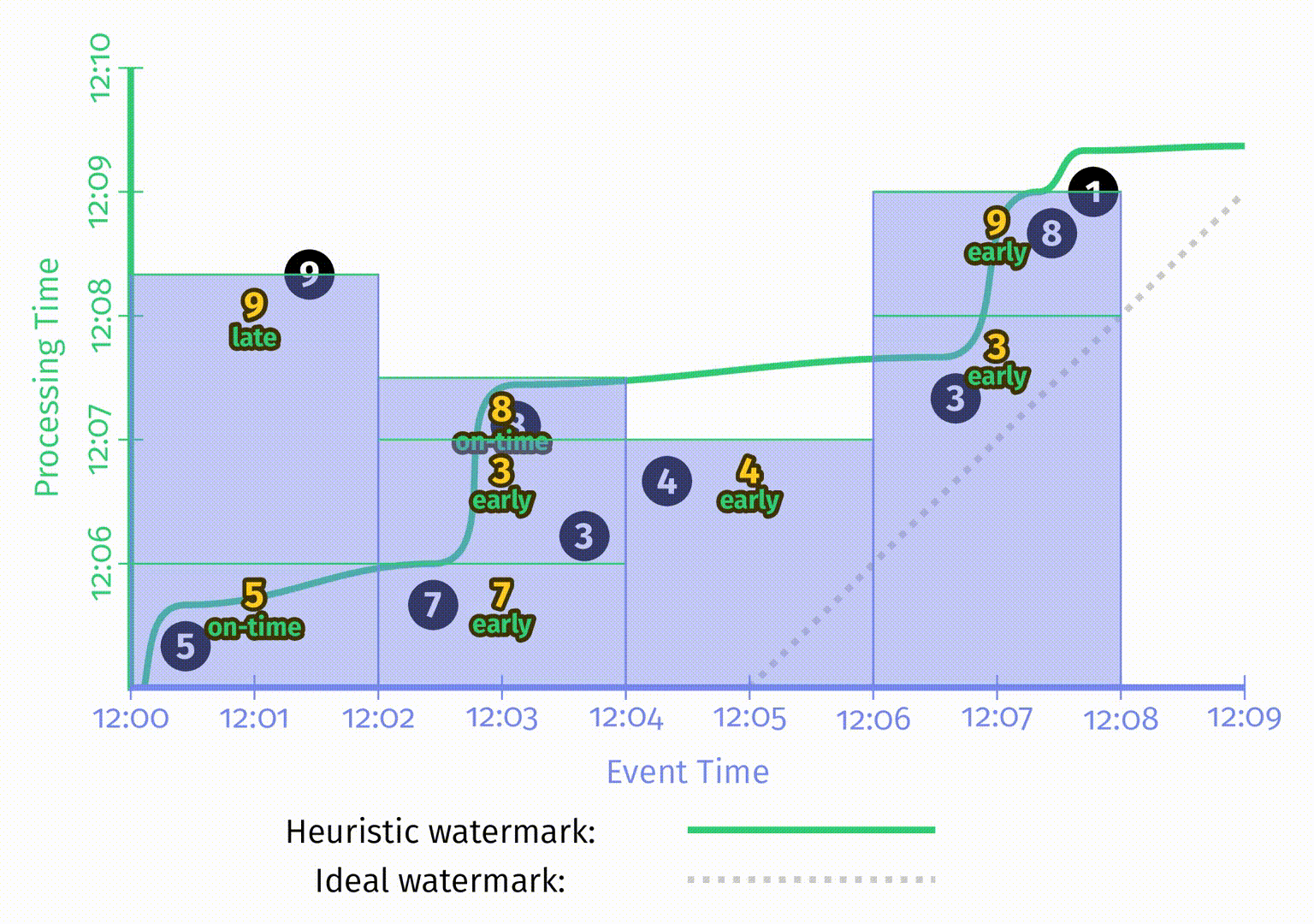
与 Figure 2-11 中积累模式的整体形状类似，但在这里所有矩形区域是不相互重叠的。

撤销模式样例如下：

PCollection<KV<Team, Integer>> totals = input
	.apply(Window.into(FixedWindows.of(TWO_MINUTES)))
		.triggering(AfterWatermark()
			.withEarlyFirings(AlignedDelay(ONE_MINUTE))
			.withLateFirings(AfterCount(1))
		.accumulatingAndRetractingFiredPanes())
	.apply(Sum.integersPerKey());

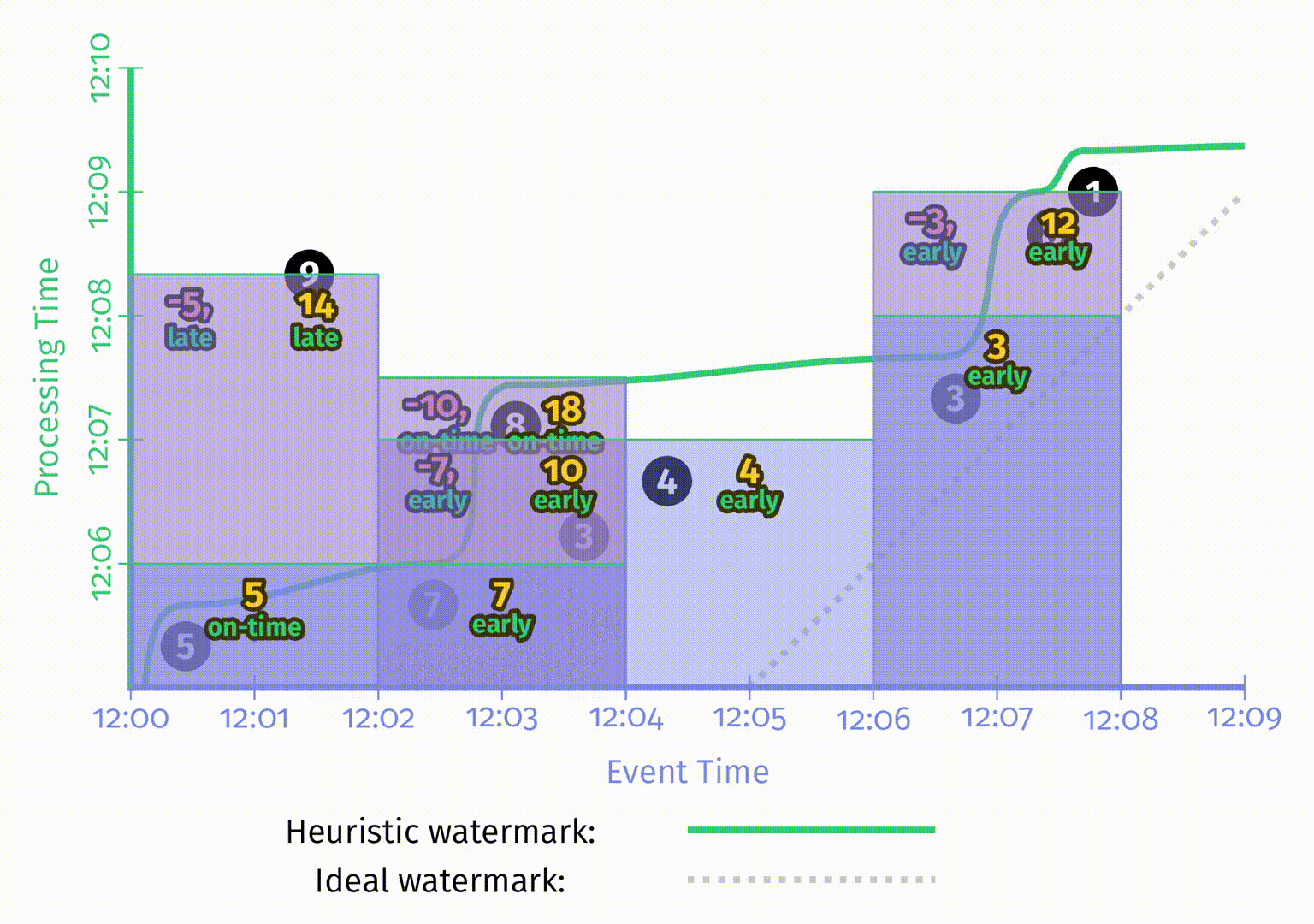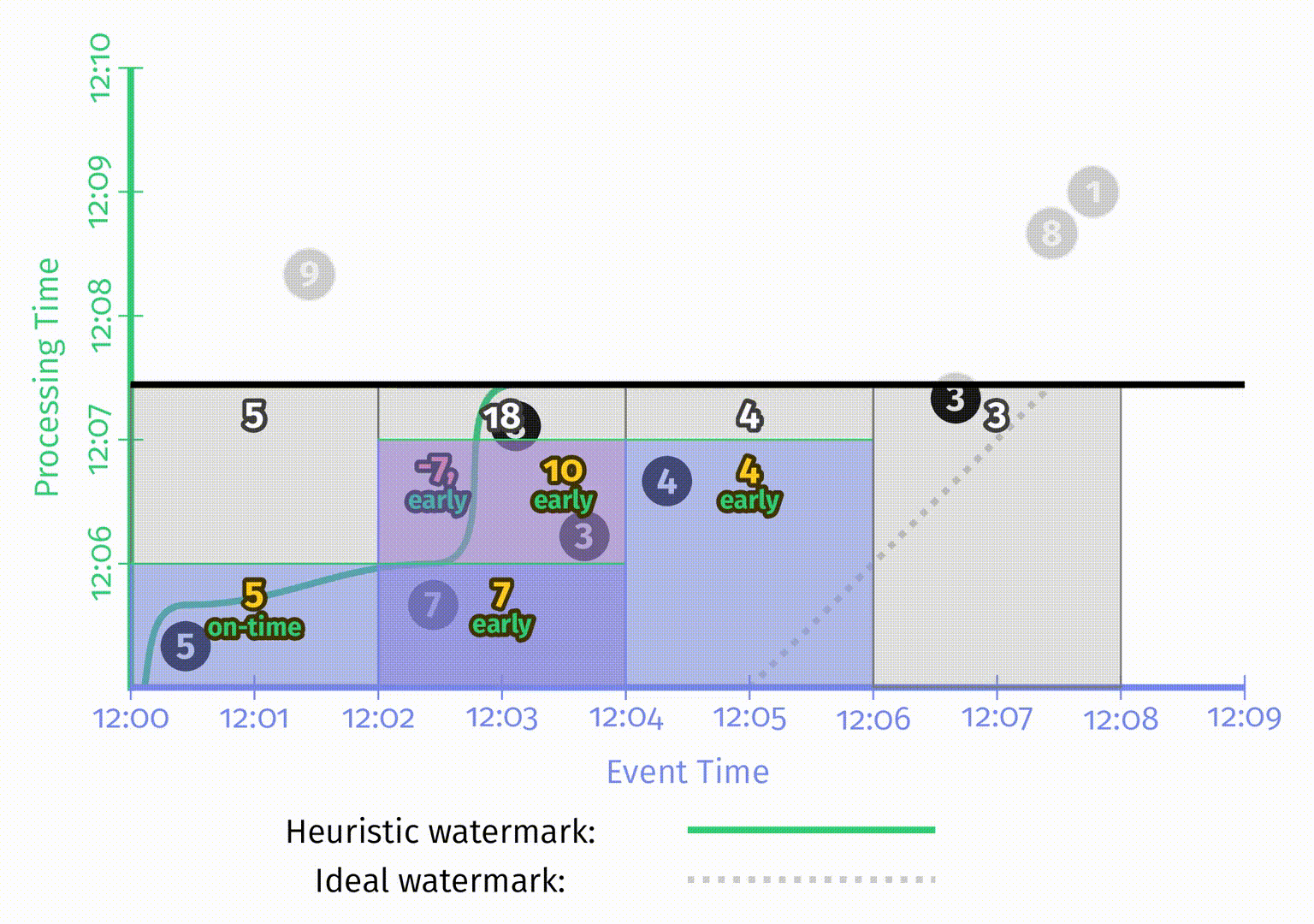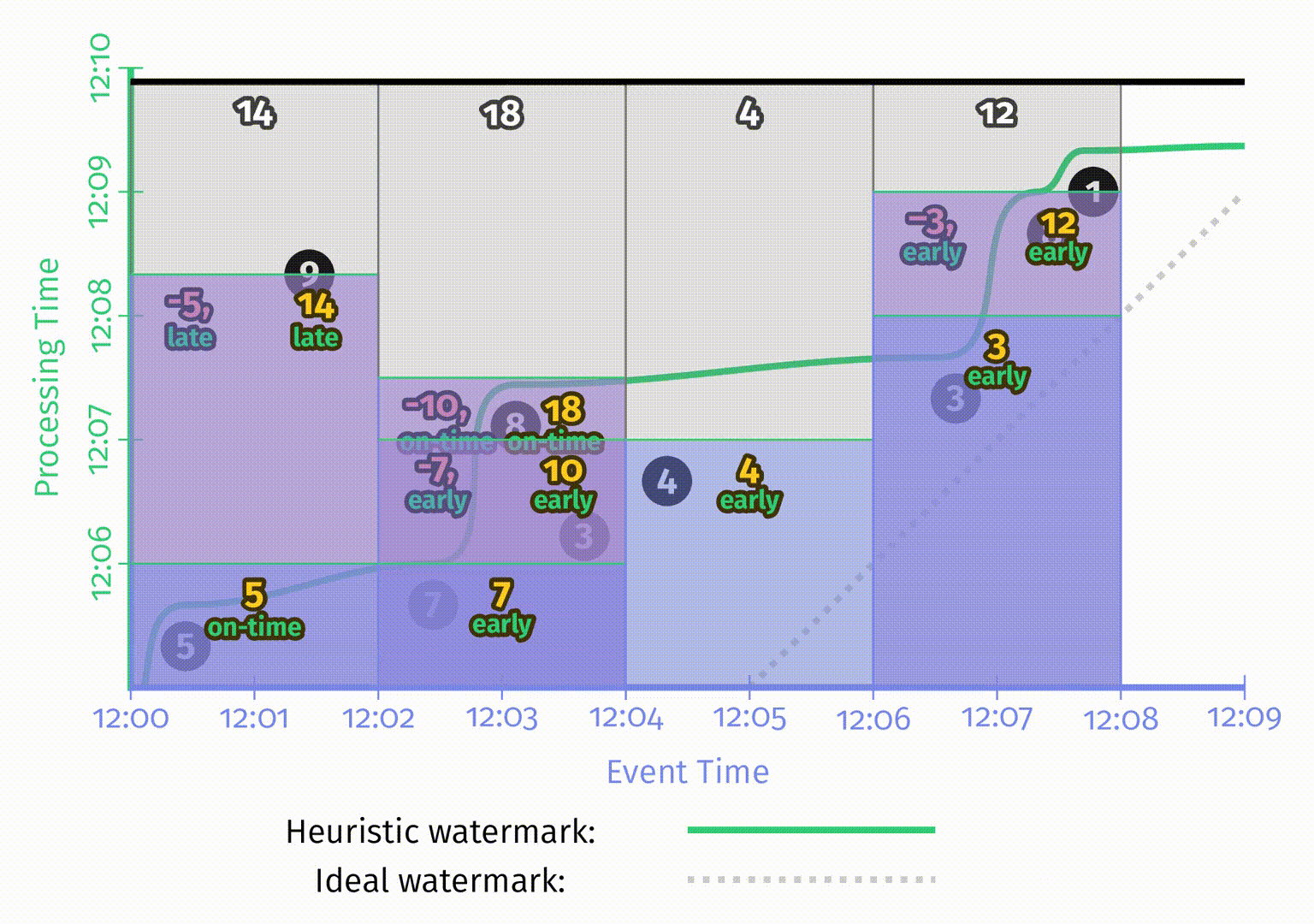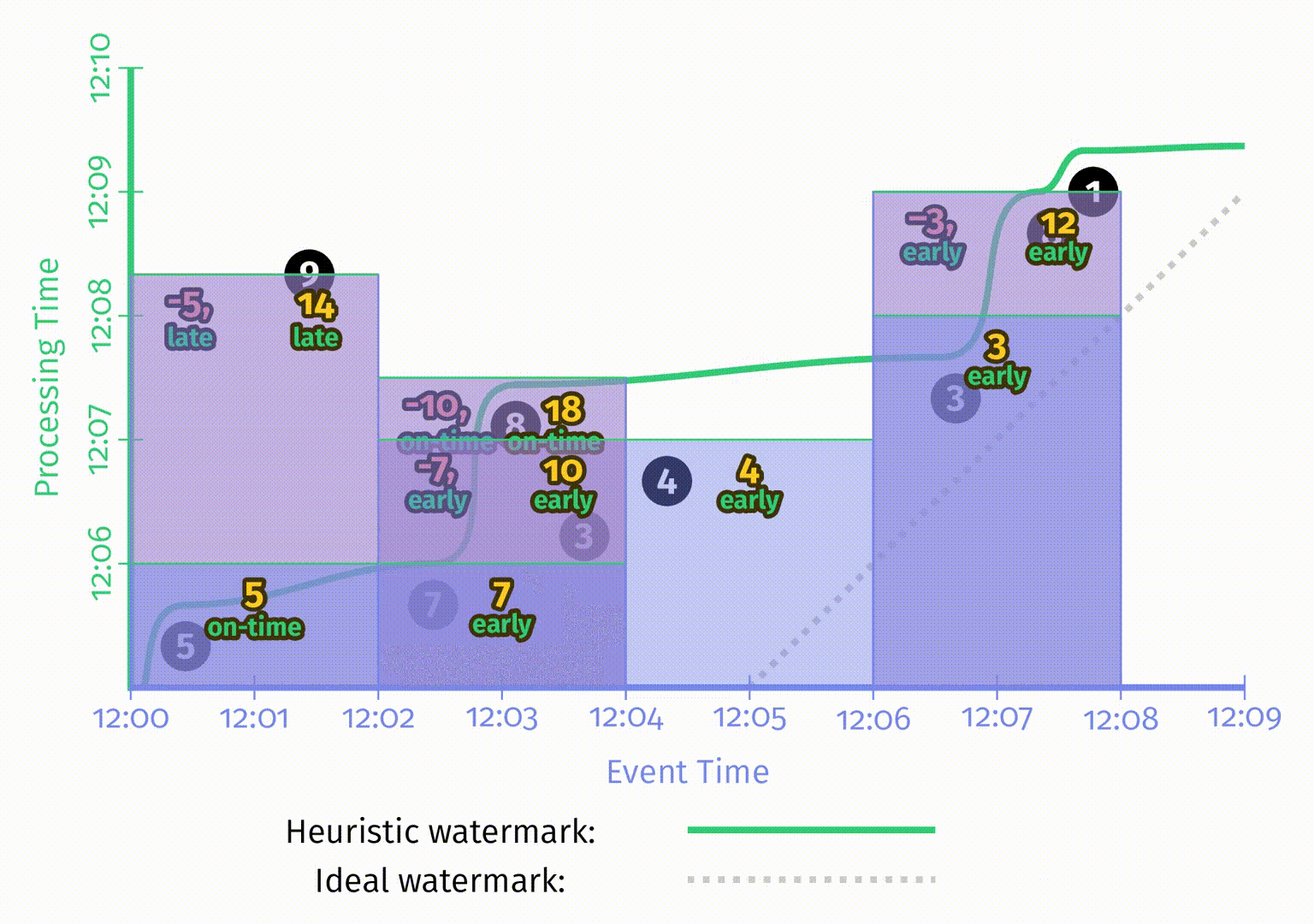
图中的撤销使用红色矩形，由于与蓝色的矩阵重叠，因此看起来有点像紫色。矩形中两个输出值之间用逗号隔开以便区分。

最后是三种模式的最后一帧对比图：

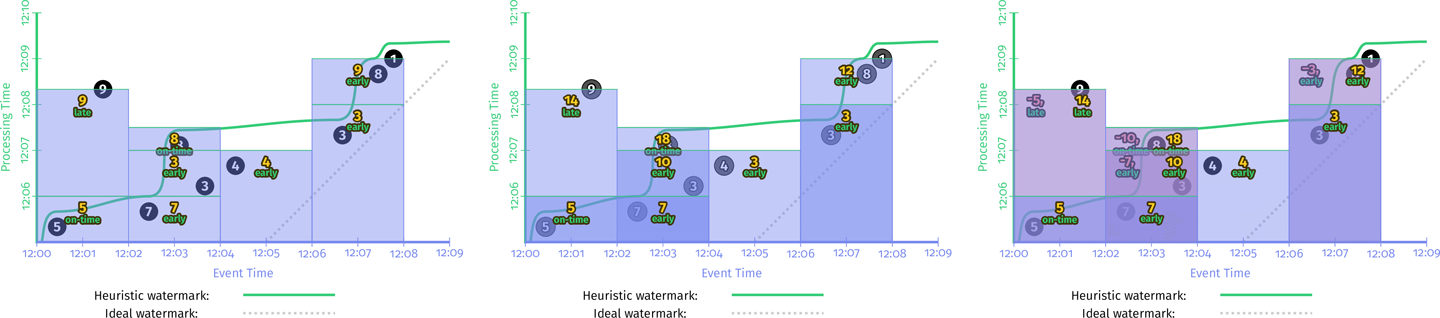
关于存储和计算的成本开销，图中的三种模式从左到右是依次递增的。聚合模式的选择提供了在正确性、延迟和开销之间权衡的另一个维度。